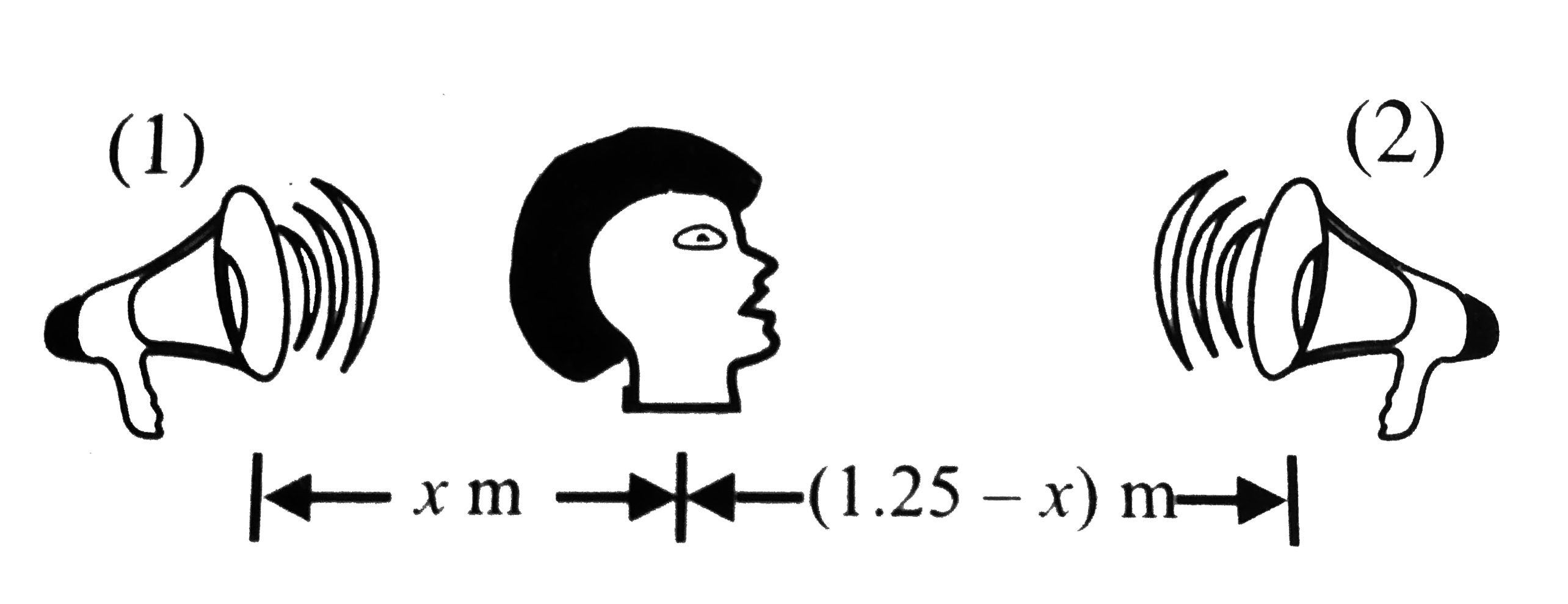Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two identical loudspeakers are driven in phase by a common oscillator ...
Text Solution
|
- Two loudspeakers are arranged facing each other at some distance. Will...
Text Solution
|
- Two points are located at a distance of 10 m and 15 m from the source ...
Text Solution
|
- Two sound sources oscillate in phase with a frequency of 100 Hz. At a ...
Text Solution
|
- Two identical loudspeakers are placed on a line at distance 4m and 6m ...
Text Solution
|
- Two identical loudspeakers are located at point A & B, 2 m apart. The ...
Text Solution
|
- Two identical loudspeakers placed 3.00 m apart are driven by the same ...
Text Solution
|
- Two identical loudspeakers are driven in phase by a common oscillator ...
Text Solution
|
- दो लाउडस्पीकर एक-दूसरे की ओर मुँह कर कुछ दूरी पर रखे हैं । क्या एक लाउ...
Text Solution
|