Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
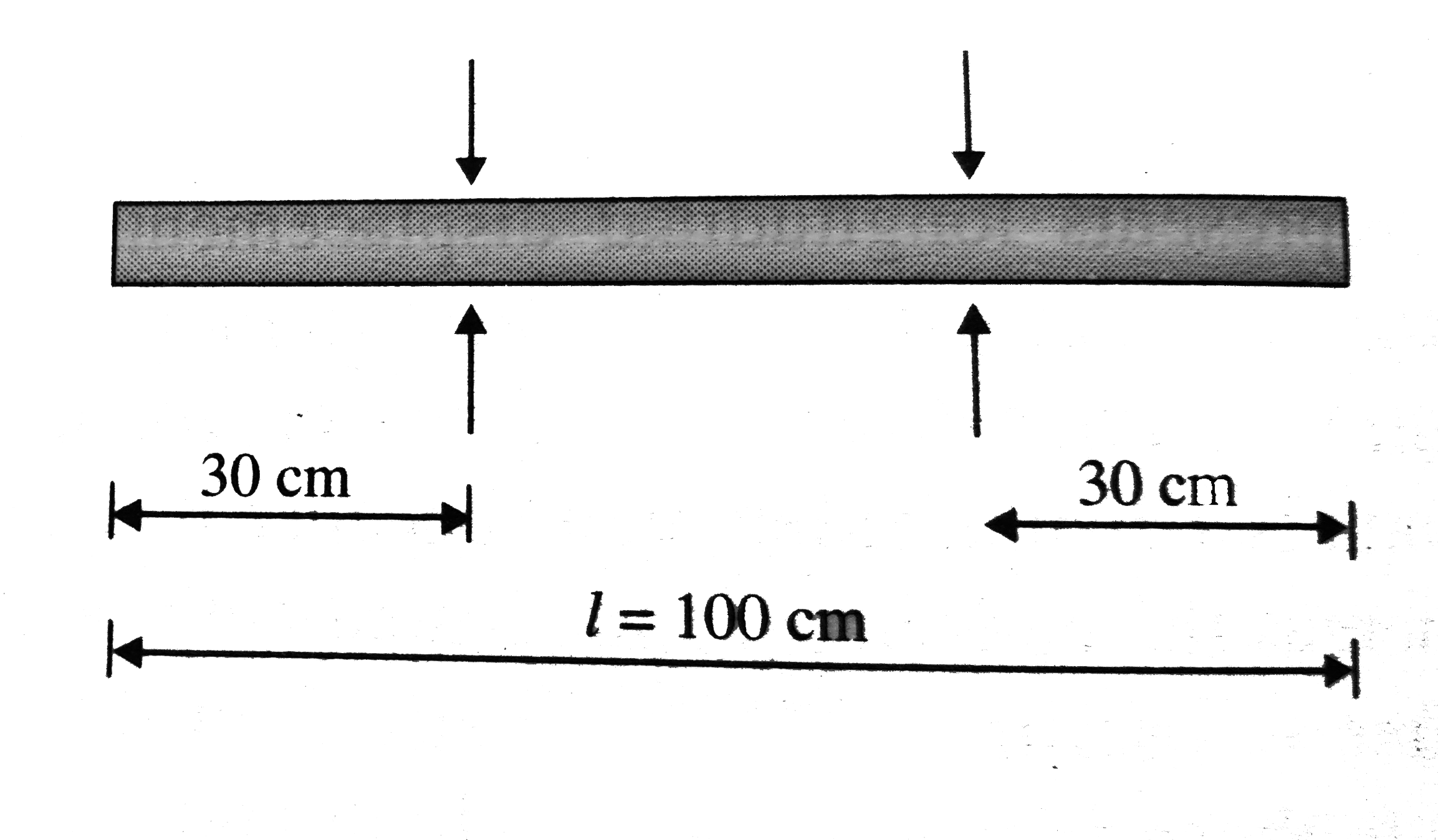
- A metal rod length l=100 cm is changed at two points A and B as shown ...
Text Solution
|
- A metal rod of length 1m is clamped at two points as shown in the figu...
Text Solution
|
- A rod of nickel of length l is clamped at its midpoint . The rod is st...
Text Solution
|
- A brass rod (density 8.3 g//cm^(3)), 3m long is clamped at the centre...
Text Solution
|
- A copper rod of length l=50 cm is clamped at its midpoint. Find the nu...
Text Solution
|
- A closed orgain pipe of length l(0) is resonating in 5^(th) harmonic m...
Text Solution
|
- An aluminium rod having a length 100 cm is clamped at its middle point...
Text Solution
|
- A metal rod length l=100 cm is changed at two points A and B as shown ...
Text Solution
|
- A metallic rod of length 1 m, young's modulus 3xx10^(11)Nm^(-3) and de...
Text Solution
|