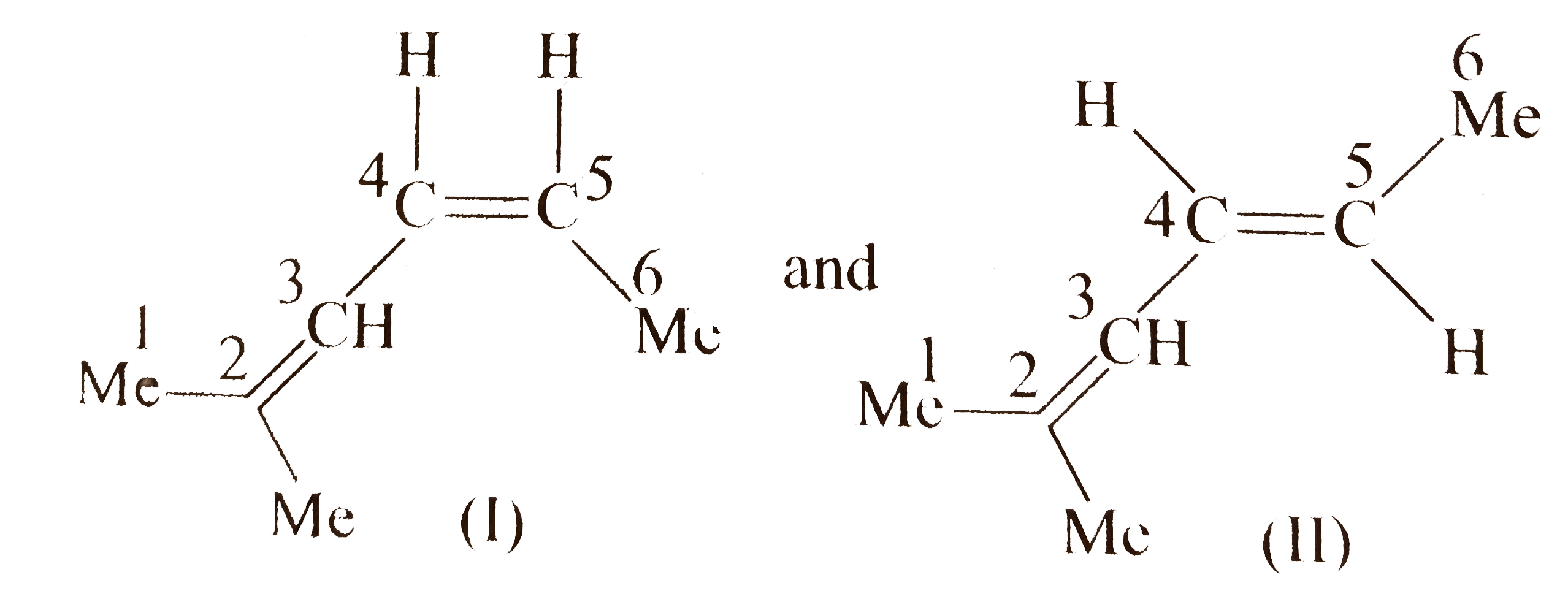In all the problem `:`
`1.` The aldehydes obtained in reductive ozonolysis are converted to acids in oxidative ozonolysis and ketones remain unchanged. So, firest convert acids into aldehyde and find the structure of `(A)`.
`2.` Keep the bi`-` functional compound in centre and other two compounds on either side with their functional groups facing each other.
`3.` If bi`-` functional compound is symmetrical, e.g., oxalic acid, one structural isomer will be obtained.
`4.` If bi`-` functional compoound is unsymmetrical, e.g., pyruvic acid, two structural isomers will be obtained.
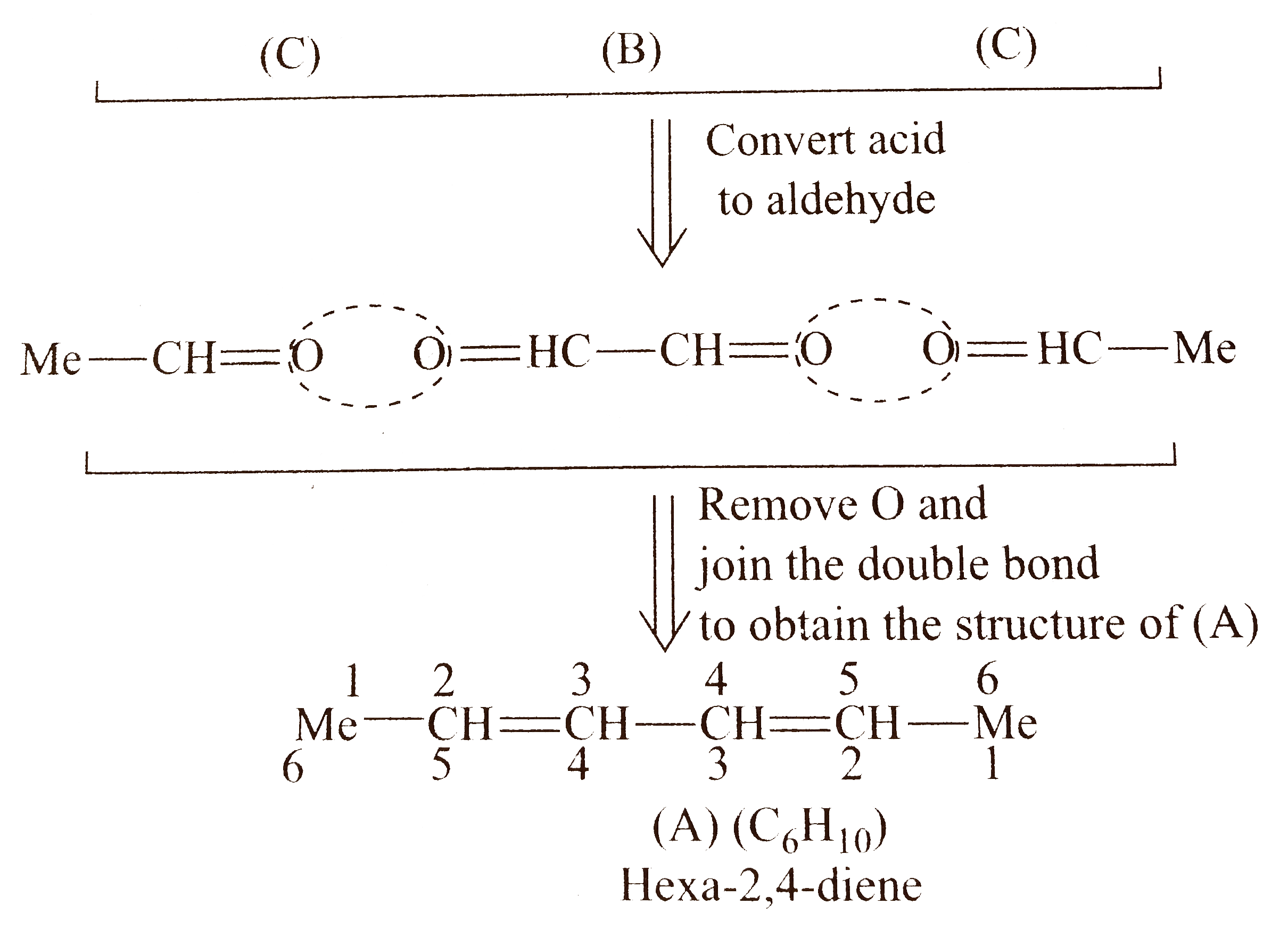
`5.` Compound `(A)` in all the parts has `2^(@)` of unsaturation and three compounds are obtained after ozonolysis, therefore, compound `(A)` in all the parts has two `(C=C)` bonds, i.e., all are dienes.
`a.`
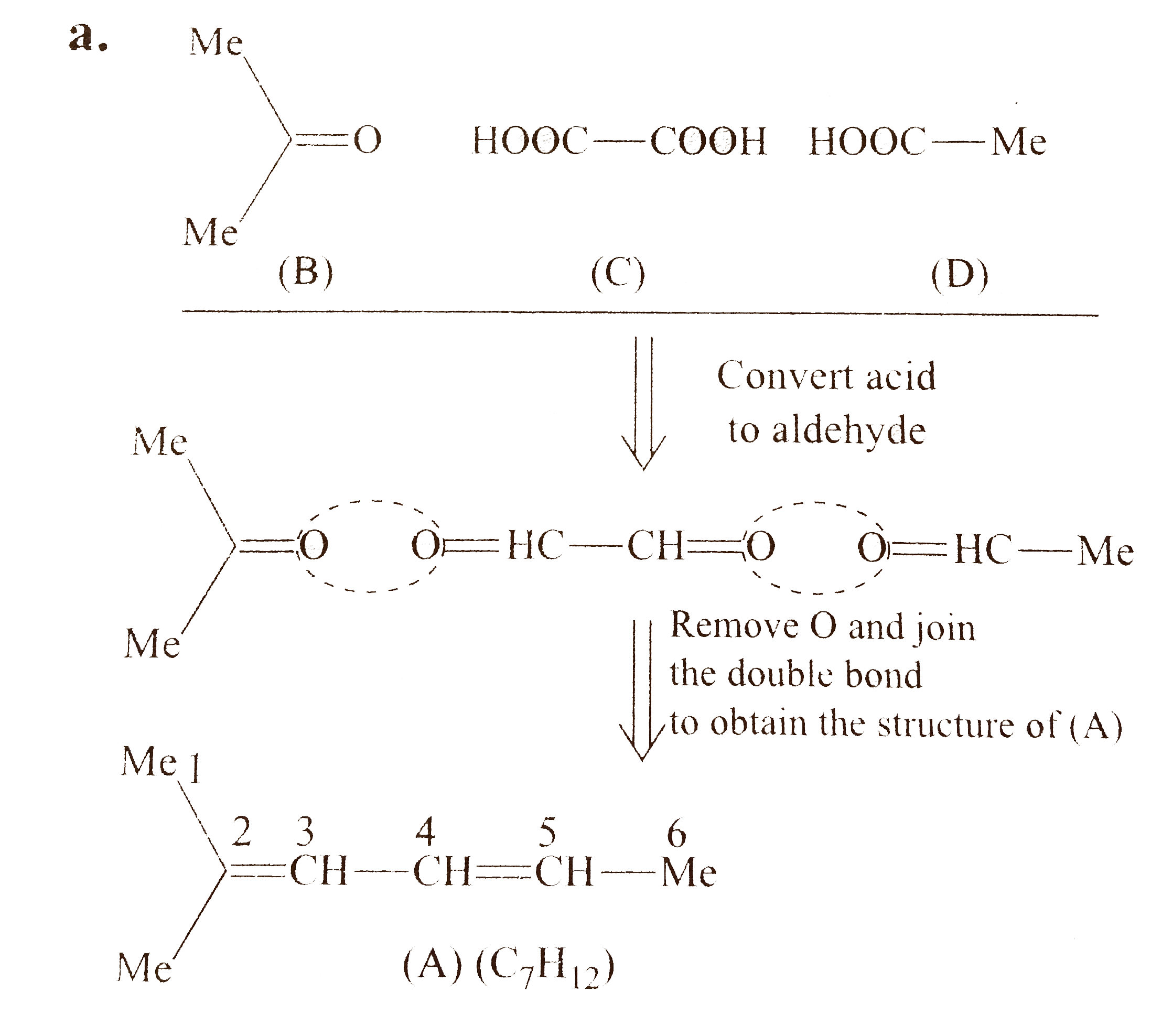
Compound `(A)` shows geometrical isomers around `C_(4)-C_(5)` double bond since the two groups around `C-4` and `C-5` are different but do not show geometrical isomers around `C_(2)-C_(3)` double bond since the two groups around `C-2` are the same.
Number of stereoismers for `(A)=2`
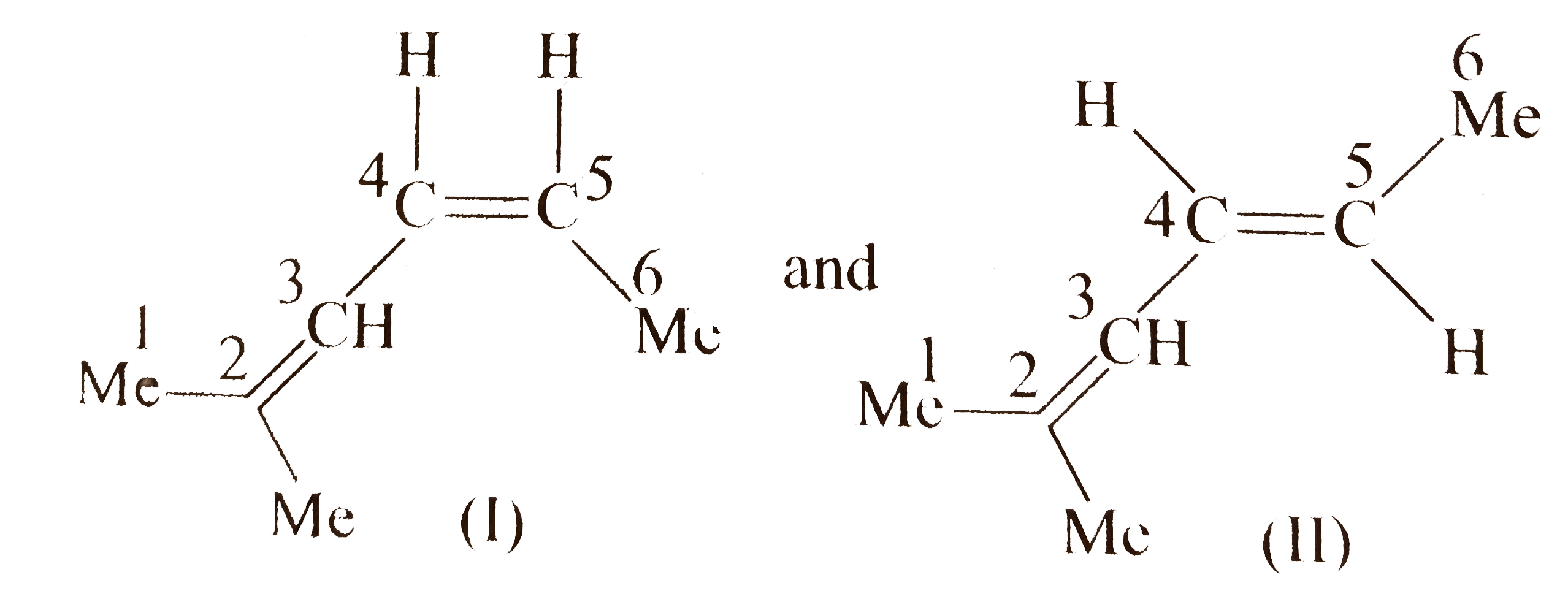
b. Proceed in the same manner as in `(a)`.
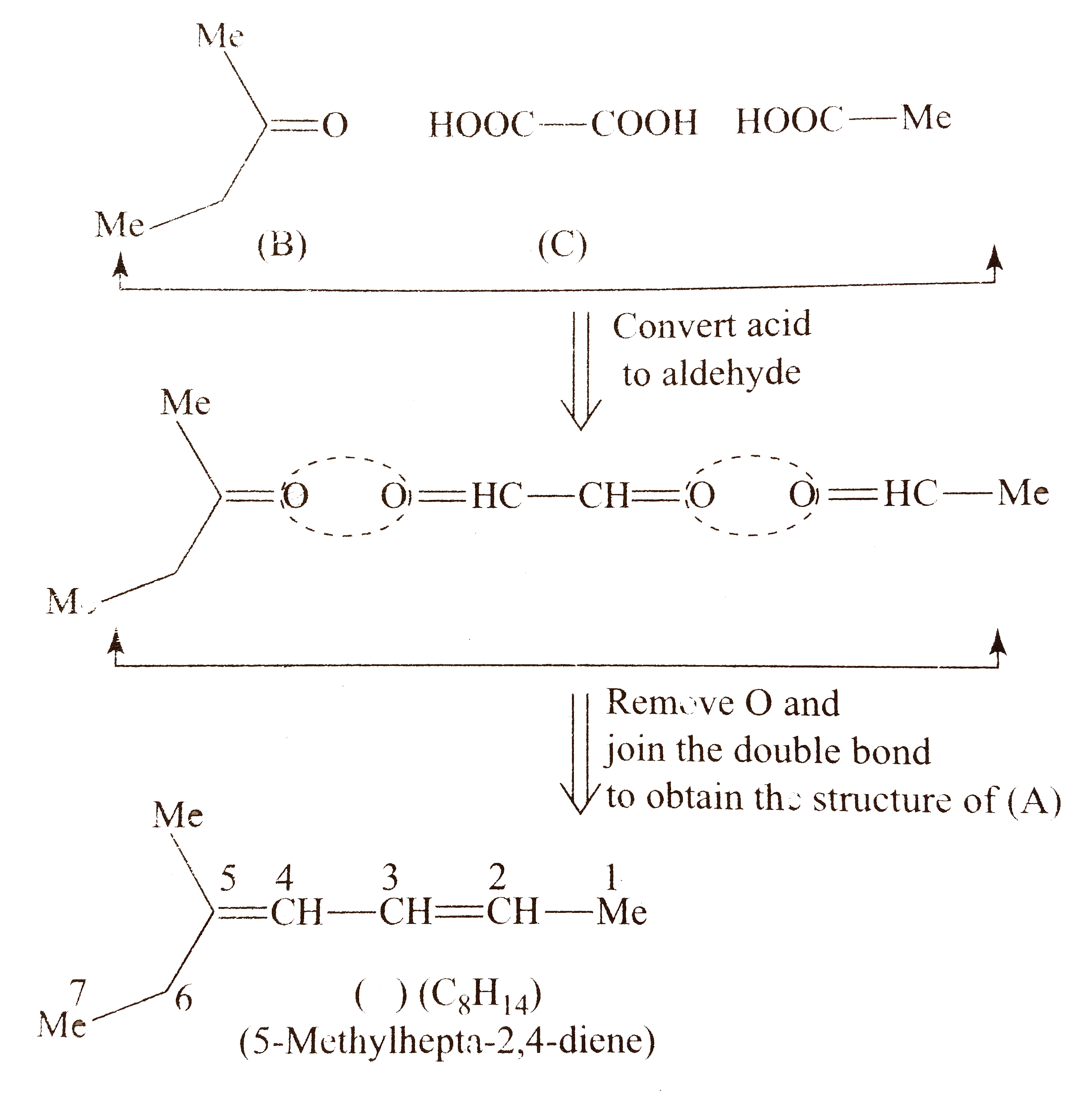
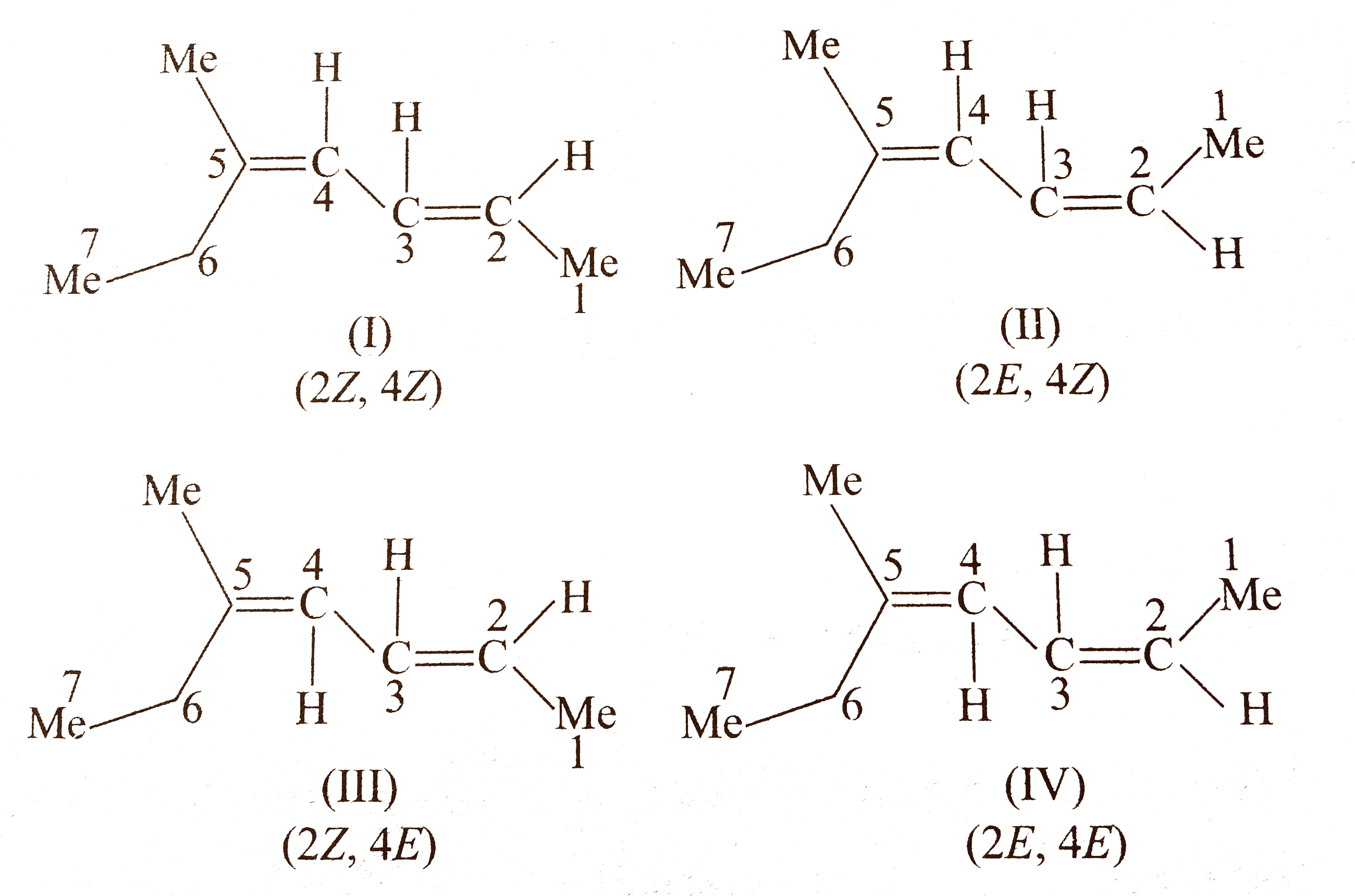
Compound `(A)` shows geometrical isomer around both `(C_(2)-C_(3))` and `(C_(4)-C_(5))` double bonds since two of the groups around these bonds are different. Moreover, terminal groups `(-CH_(3))` and `(-C_(2)H_(5))`, around `C_(2)` and around `C_(5)` , respectively, are different.
Number of `G.I.` when the terminal groups are different `=2^(n),` where`n` is the number of double bonds (two double bonds).
` :. G.I. =2^(2)=4`
Number of stereoismoers of `(A)=4`
`c.` Proceed in the same maner as in `(a)` and `(b)`
Total `C` atoms in `(A)=6`
Total `C` atoms in `(B)+(C)=4`
Therefore, there must be `2 mol ` of monofunctional compoound (C) (acetic acid).
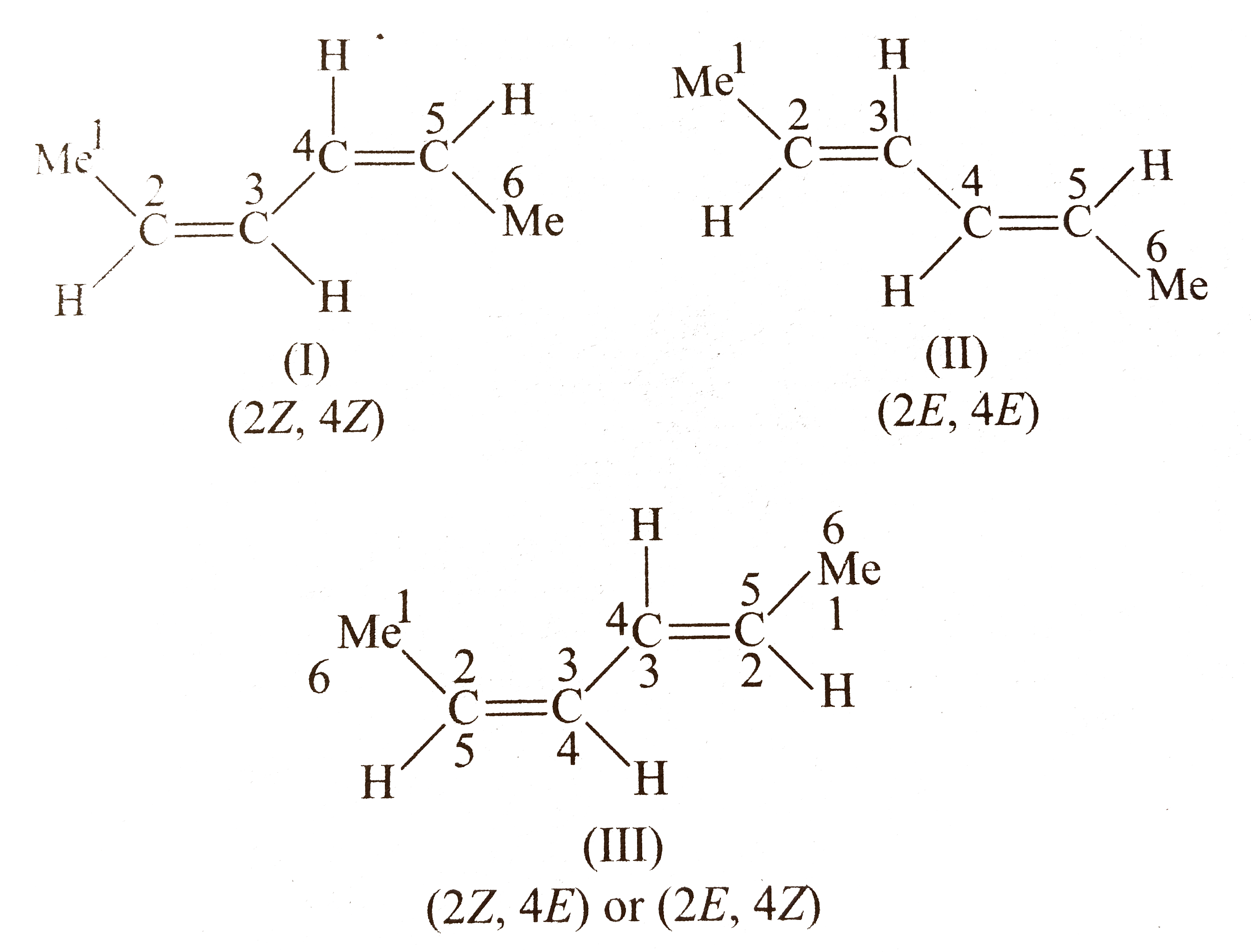
Compound `(A)` shows geometrical isomerism around both `(C_(2)-C_(3))` and `(C_(4)-C_(5))` double since the two groups around these double bonds are different. Moreover, the terminal groups around `C_(2)` and around `C_(5)` are same (methly group).
Number of `G.I.` when the terminal groups are the same.
`=overset(n-1)(2)+overset((n-2)//2)(2)`, where `n` is the number of double bonds and `n` is even.
`G.I.=2 ^(n-1)+2^(2)`
Number of stereoisomers of `(A)=3`
(Here,` 2Z,4E`and `2E,4Z` will be the same, since the numbering can be one either way.)
`d.` Procedd in the same manner as in `(a),(b)`, and (c). Here, the bi - functional group compound `(C)` is unsymmetrical, therefore, there will be two structureal isomers of `(A)` and each of them will show stereoisomers.
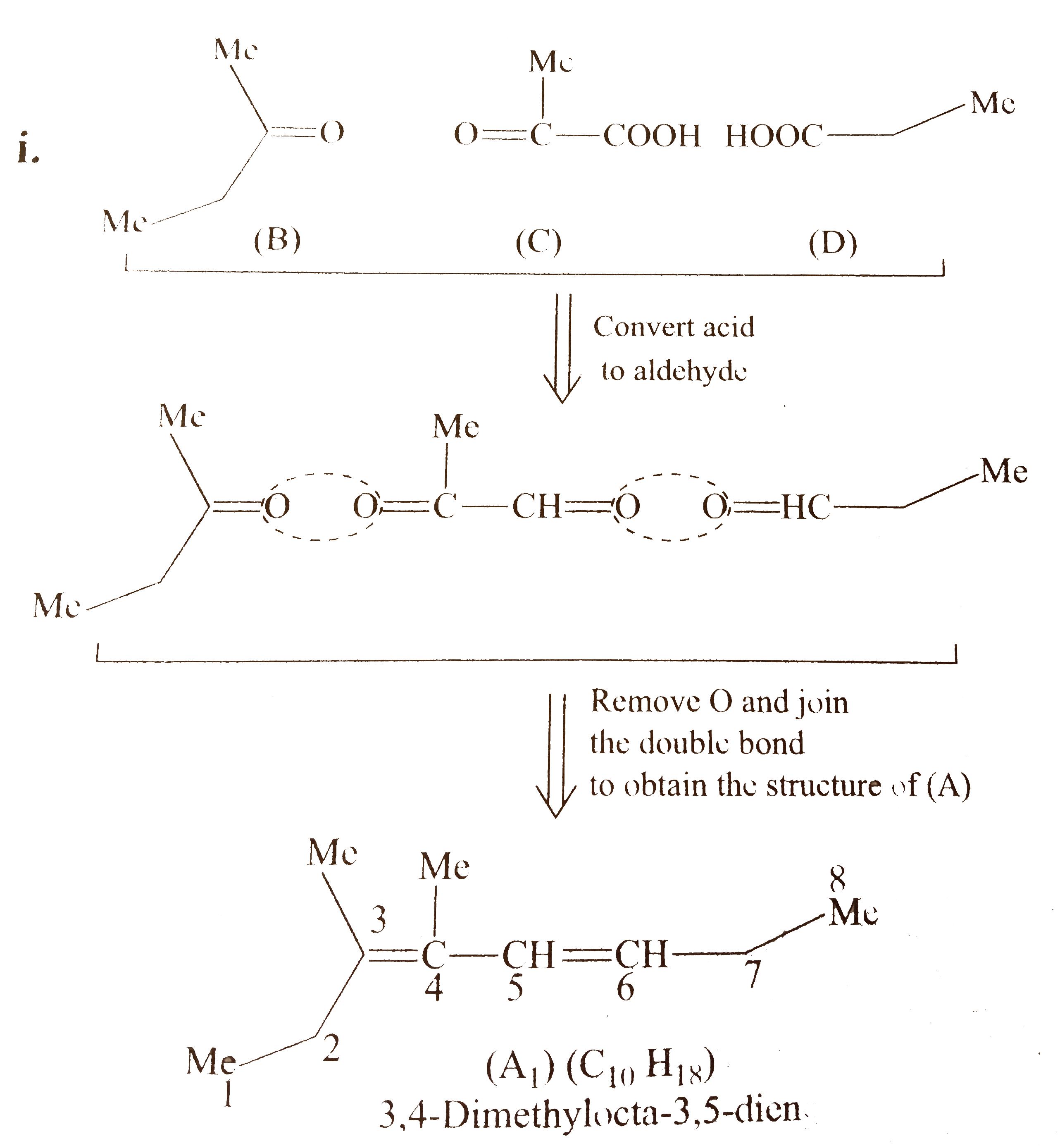
`i.`
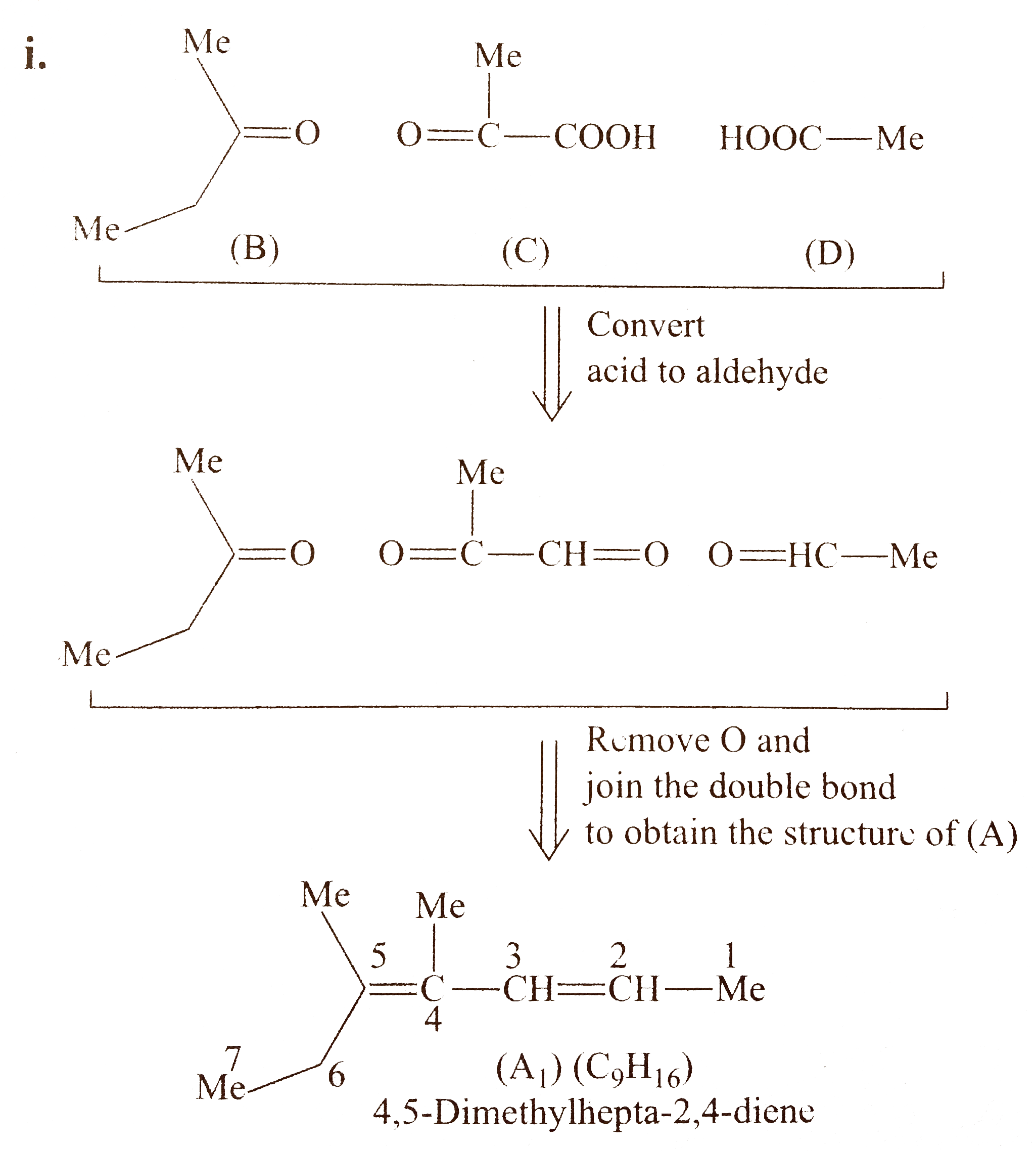
`ii.` Another structural isomer of `(A)` is possible, by either changing the position of `(B)` and `(D)` or by writing the structure of `(C)` in another way [pointing `(-COOH)` group in `(C)` towards (B)].


Both `(A_(1))` and `(A_(2))` show geometrical isomers around `(C_(2)-C_(3))` and `(C_(4)-C_(5))` double bonds, because the two groups around these double bonds are different. Moreover, the terminal groups around `C_(2)` and `C_(5)` are different (at `C-2,` one `Me` and `H,` at `C_(6)` one `Me` and one `Et` group) .
Number of `G.I.` when terminal groups are different `=2^(n)=2^(2)=4`
Hnece, `(A)` will show four geometrical isomers, similarly, `(A_(2))` will also show four geometrical isomers.
Number of stereoisomers for `(A)=(A_(1)+A_(2))=(4+4)=8 `
Four diastereomers for `A_(1)`
`i.` `2X,4Z` `ii.` `2E,4E`
`iii.` `2E,4Z` `iv.` `2Z,4E`
`e.` Proceed in the same manner is in `(a)`. The bi`-` functional groups compound `(C)` is uncymmetrical, therefore, there wil be two structural and each of them will show stereoisomers.
`i.`
`ii.` Another structural isomer of `(A)` is possible by either changing of `(B)` and `(D)` or by writing the structure of `(C)` in another way `[` pointing `(-COOH)` group in `(C)` towards `(B)]`.
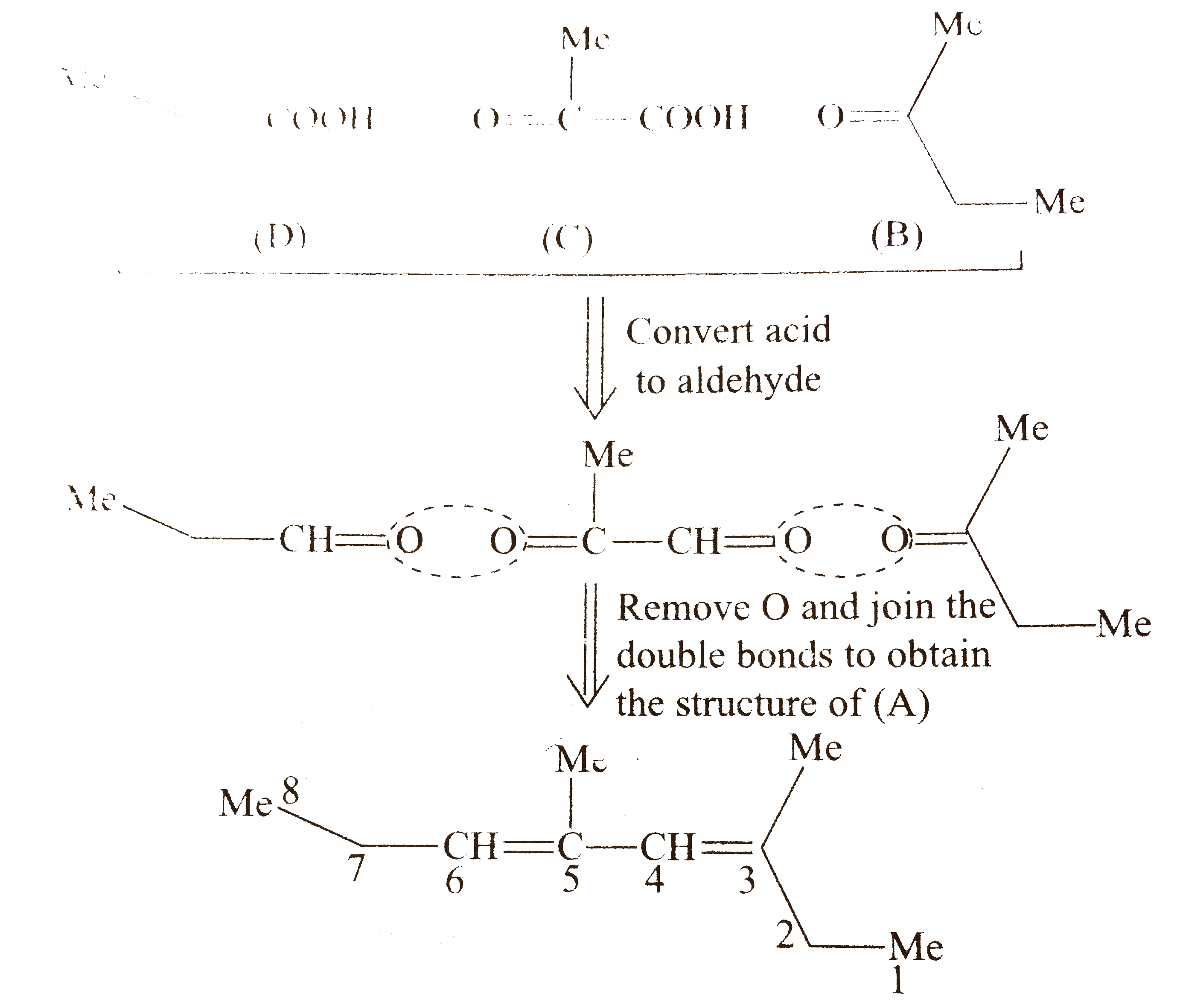
Both `(A_(1))` and `(A_(2))` show `G.I.` around `(C_(3)-C_(4))` and `(C_(5)-C_(6))` double bonds, because the two groups around these double bonds are different. Moreover, the terminal groups `C_(3)` and `(C_(6))` are different `(` at `C_(3)`, one `Me` and one `Et` group, at `C_(6)` one `Et` and one `H)`
Number of `G.I.` when the terminal groups are different `=2^(2)=4`.
Number of diastereomers for `(A_(1))=4`
number of diastereomers for `(A_(2))=4`
Total number of stereoisomers `=8`