Home
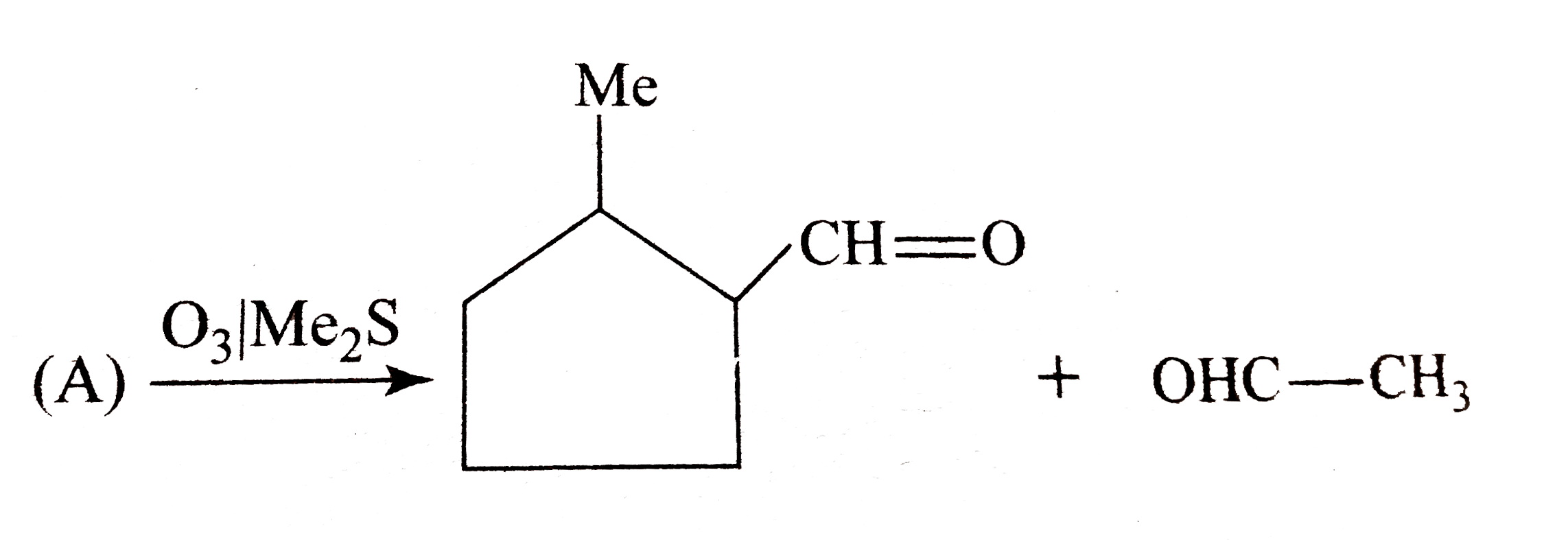
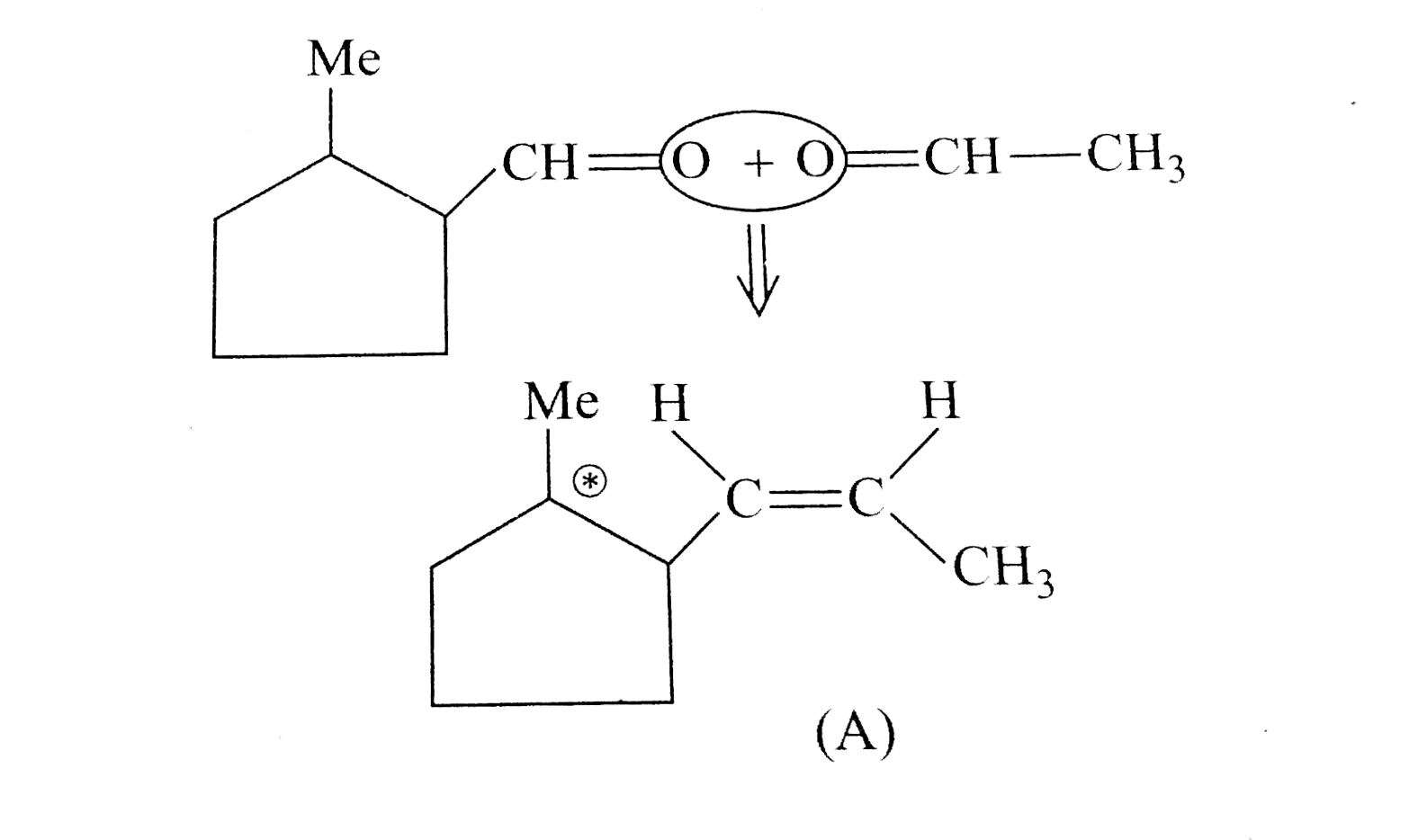
Class 11
CHEMISTRY
The number of geometrical isomers of (A)...


The number of geometrical isomers of `(A)` can be `:`

A

a. 2

B

b. 3

C

c. 4

D

d. 5

Text Solution

Verified by Experts

The correct Answer is:
c
Proceeding reverse, the structure of `(A)` is `:`

`(A)` has one asymmetric `C` atom `implies` two optical isomers and has one `(C=C)` with two different groups `implies` geometrical isomers.
Total number of stereoisomers `=4`.
Promotional Banner

Topper's Solved these Questions

  • ALKENES AND ALKADIENES

    CENGAGE CHEMISTRY ENGLISH|Exercise Archives(ASSERTION-REASIOING)|4 Videos

  • ALKENES AND ALKADIENES

    CENGAGE CHEMISTRY ENGLISH|Exercise Fill in the Blanks|3 Videos

  • ALKENES AND ALKADIENES

    CENGAGE CHEMISTRY ENGLISH|Exercise Multiple Correct Answer Type|41 Videos

  • ALKANES AND CYCLOALKANES

    CENGAGE CHEMISTRY ENGLISH|Exercise Archives|13 Videos

  • ALKYNES

    CENGAGE CHEMISTRY ENGLISH|Exercise Exercises (Archives - Analytical and Desriptive Type)|4 Videos

Similar Questions

Explore conceptually related problems

Number of geometrical isomers possible of

The number of geometrical isomers of the compound is C_(6)H_(5)-CH=CH-CH=CH-COOH

The number of geometrical isomers of the complex [Co(NO_(2))_(3) (NH_(3))_(3)] is

For the complex [Fe(en)_(2)Cl_(2)]Cl (en = ethylene diamine ) , identify (i) the oxidation number of iron , (ii) the hybrid orbitals and the shape of the complex, (iii) the magnetic behaviour of the complex , (iv) the number of geometrical isomers , (v) whether there is an optical isomer also , and (vi) name of the complex . (At. no. of Fe = 26)

The number of geometrical isomers in CH_(3)CH=N-OH is

Geometrical isomers differ in

The number of geometric isomers that can exist for square planar [Pt(C1)(py)(NH_(3)) (NH_(2)OH)^(+)] is (py = pyridine).

The number of geometric isomers that can exist for square planar [Pt(C1)(py)(NH_(3)) (NH_(2)OH)^(+)] is (py = pyridine).

Which can show geometrical isomer ?

Which is the pair of geometrical isomers :