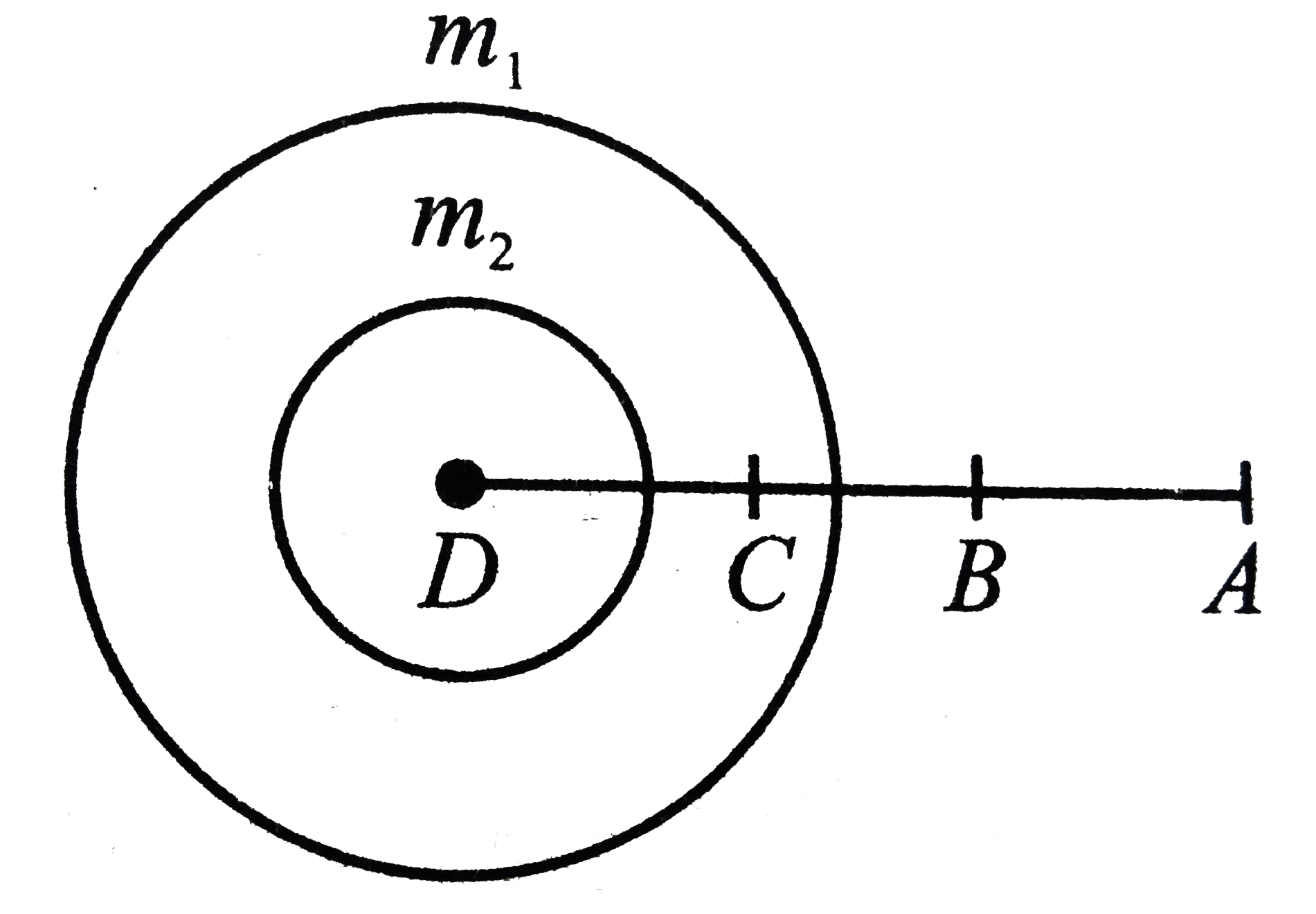
Figure shows two shells of masses `m_(1)` and `m_(2)`. The shells are concentric. At which point, a particle of mass `m` shall experience zero force?

Two concentric shells of mass m_(1) and m_(2) are situated as shown. Find the force on a particle of mass m when the particles is located at (a) r=r_(1),(b)r=r_(2),(c)r=r_(3) . The distance r is measured from the centre of the shell.

The figure shows a spherical shell of mass M . The point a is not at the centre but away from the centre of the shell. If a particle of mass m is placed at A , then

In the figure given below, two particles of masses m and 2m are fixed in place on an axis. Where on the axis can a third particle of mass 3m be placed (other than at infinity) so that the gravitational force on it from the first two particles is zero?

Two concentric shells of masses M_(1) and M_(2) are concentric as shown. Calculate the gravitational force on m due to M_(1) at points P,Q and R .

Two concentric shells of uniform density of mass M_(1) and M_(2) are situated. The forces experienced by a particle of mass m when palced at positions A,B and C respectively are given OA =p,OB = q and OC =r . .

F is the gravitational force between two point masses m_(1) and m_(2) , separated by a distance d. A point mass 2m_(1) is then brought near m_(1) . What is the total force on m_(2) ?

Two spherical shells have masses m and 2m as shows. Choose the correct options.

Two stationary particles of masses M_(1) and M_(2) are 'd' distance apart. A third particle lying on the line joining the particles, experiences no resultant gravitational force. What is the distance of this particle from M_(1) ?

Consider a system of two particles having masses m_(1) and m_(2) . If the particle of mass m_(1) is pushed towards the centre of mass of particles through a distance d , by what distance would the particle of mass m_(2) move so as to keep the mass centre of particles at the original position?