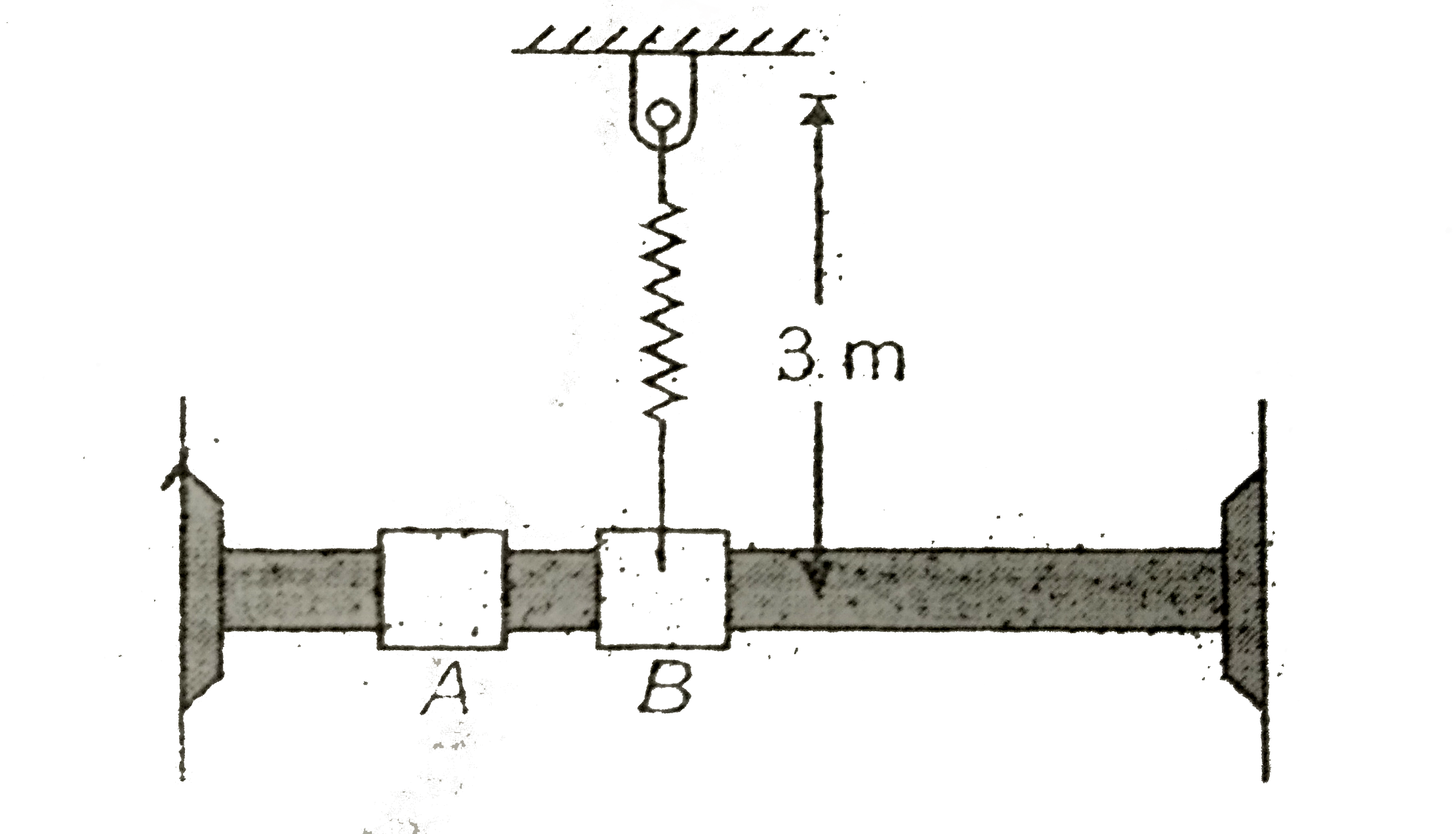Similar Questions
Explore conceptually related problems
Recommended Questions
- A collar B of mass m is at rest and when it is in the position shown, ...
Text Solution
|
- A block of mass m is connected to another block of mass M by a spring ...
Text Solution
|
- As shown in figure a smooth rod is mounted just above a table top 10 k...
Text Solution
|
- A collar B of mass 2kg is constrained to move along a horizontal smoot...
Text Solution
|
- A block of mass m is connected to another block of mass M by a massles...
Text Solution
|
- A block of mass 'm' is connected to another block of mass 'M' by a spr...
Text Solution
|
- A collar B of mass m is at rest and when it is in the position shown, ...
Text Solution
|
- A block of mass 'm' is connected to another block of mass 'M' by a spr...
Text Solution
|
- A 10 kg collar is attached to a spring (spring constant 600 N/m.), it ...
Text Solution
|