Home
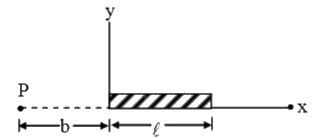
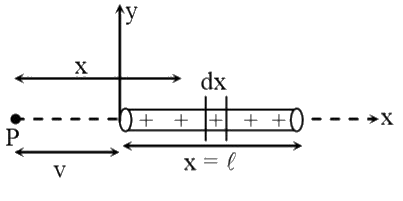
Class 11
PHYSICS
A rod of length 'l' is placed along x-a...

A rod of length `'l'` is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density `lambda=` a, a being a positive constant. Electric potential at P as shown in the figure is -

A

`(a)/(4pi epsilon_(0)) ln((b+l)/(b))`

B

`(a)/(4pi epsilon_(0)) "ln" (l)/(b)`

C

`(a)/(4pi epsilon_(0)) "ln"(b)/(l)`

D

zero

Text Solution

Verified by Experts

The correct Answer is:
A

`V= int_(b)^(b+l) (kdq)/(x) = int_(b)^(b+l) (k lambda dx)/(x) =ka int_(b)^(b+l) (dx)/(x)`
`V="Ka ln"((b+l)/(b))`
`V=(a)/(4pi epsilon_(0)) "ln"((b+l)/(b))`
Promotional Banner

Similar Questions

Explore conceptually related problems

A rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density lambda=(a)/(x) , a being a positive constant. The electric potential at the point P (origin) as shown in the figure is

A rod of length L lies along the x-axis with its left end at the origin. It has a non-uniform charge density lamda=alphax , where a is a positive constant. (a) What are the units of alpha ? (b) Calculate the electric potential at point A where x = - d .

A non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is lambda = lambda_(0)x . The centre of mass of rod divides the length of the rod in the ratio:

A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is lambda=lambda_(0)x . The distance of centre of mass of rod from the origin is :

A rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density is lambda such that lambda=a+bx . Find the mass of the rod.

A rod length L and mass M is placed along the x -axis with one end at the origin, as shown in the figure above. The rod has linear mass density lamda=(2M)/(L^(2))x, where x is the distance from the origin. Which of the following gives the x -coordinate of the rod's center of mass?

A semi-infinite insulating rod has linear charge density lambda . The electric field atthe pointPshown in figure-1.418 is: