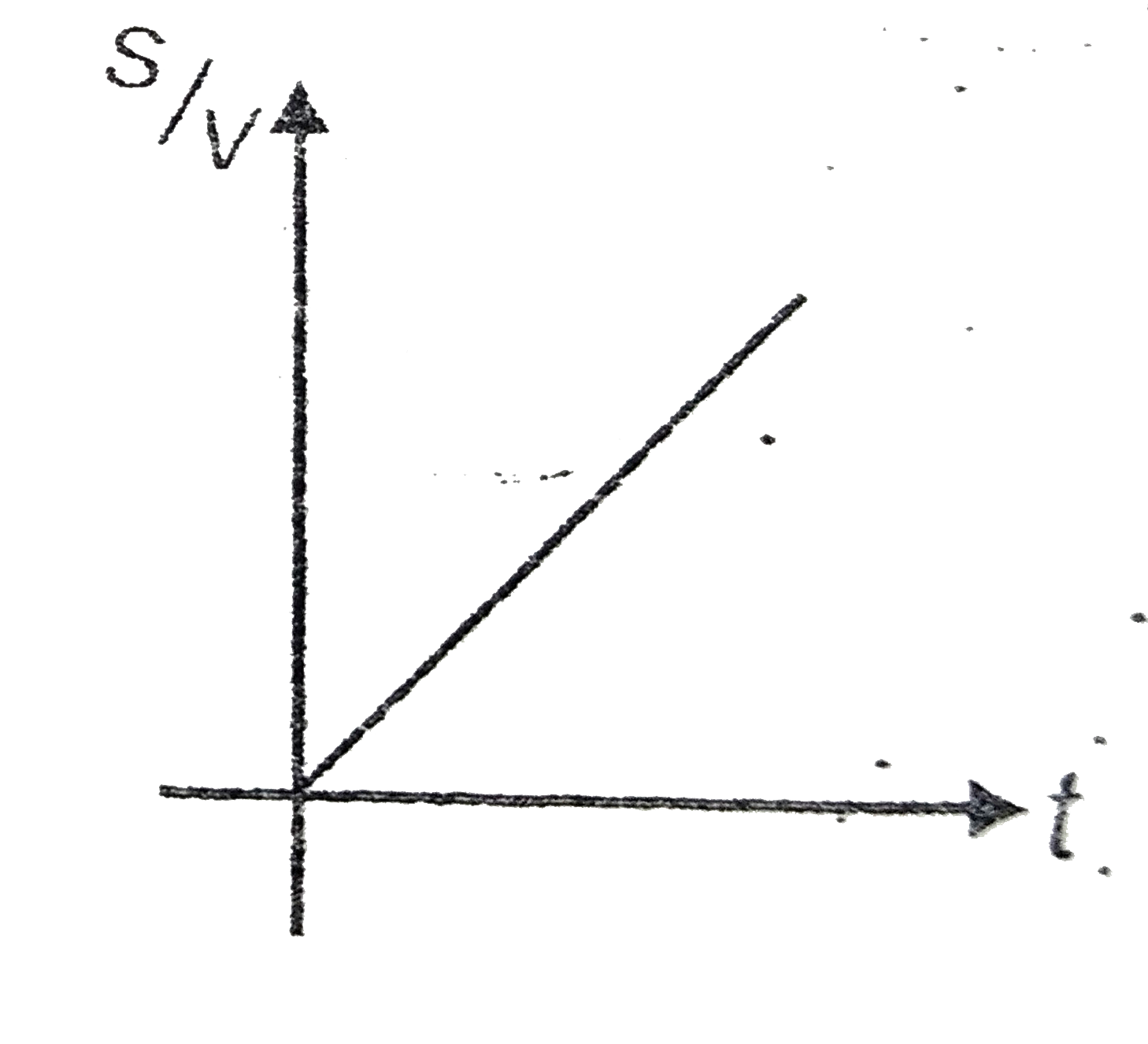
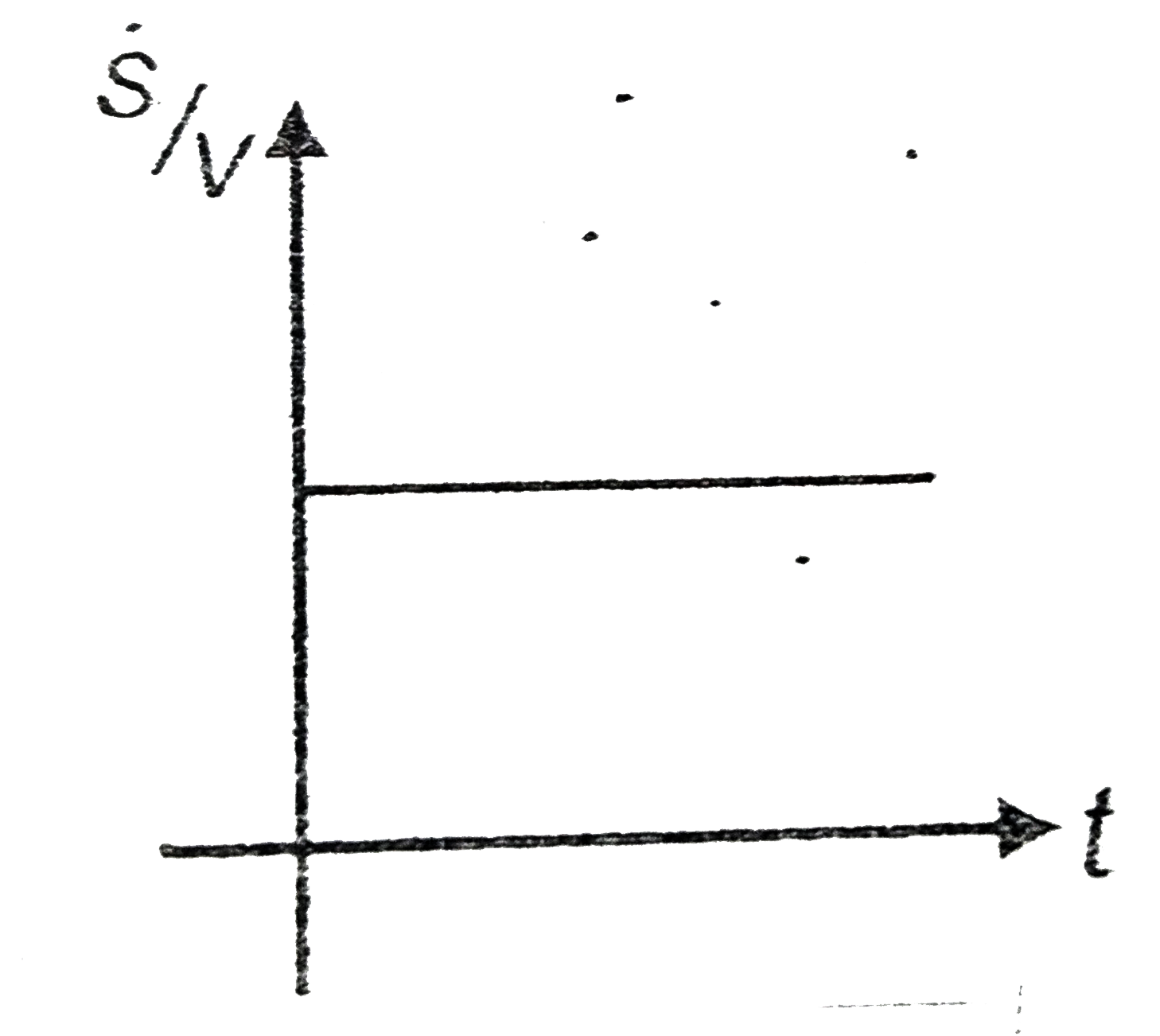
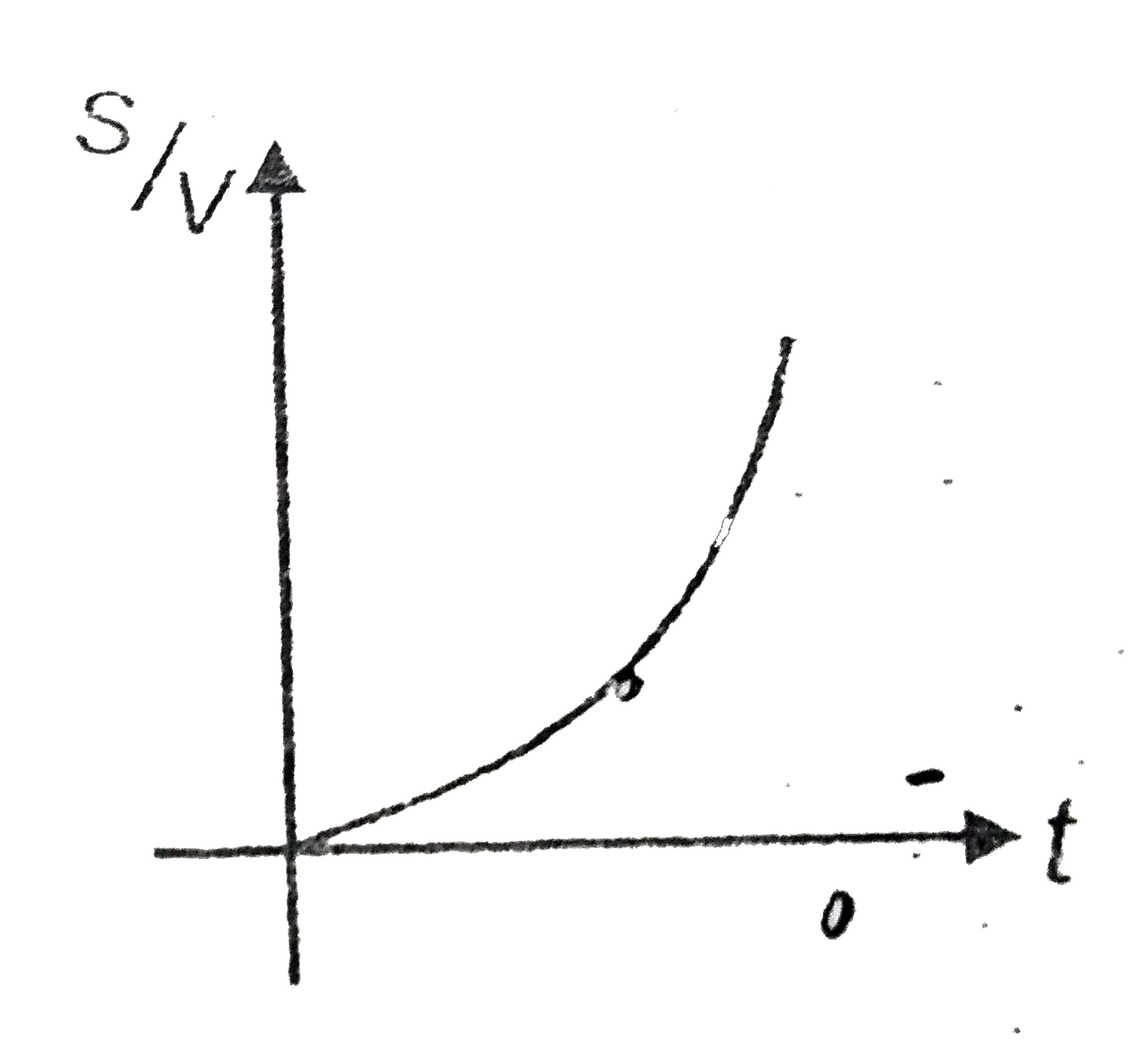
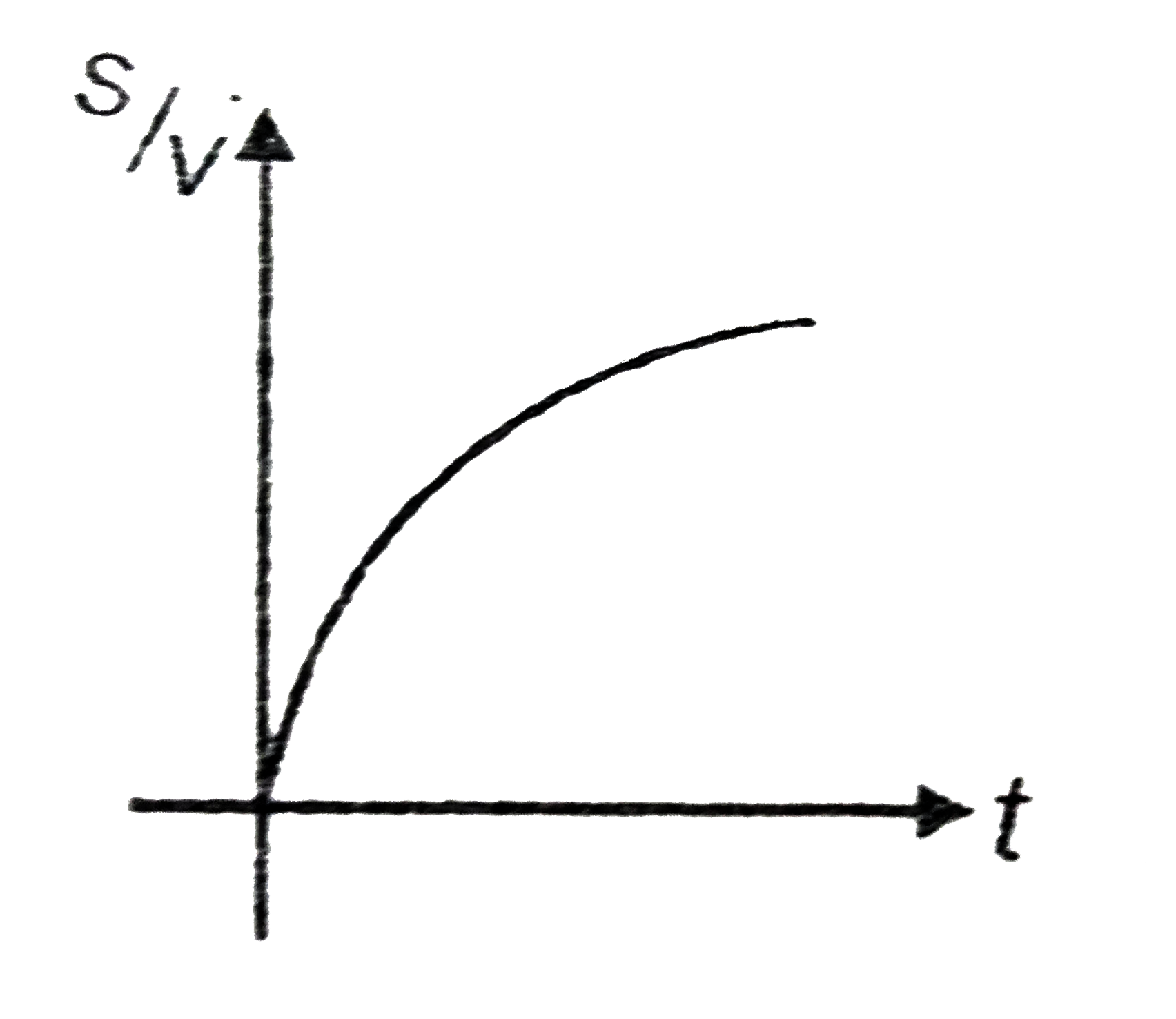
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
WORK, ENERGY AND POWER
AAKASH INSTITUTE ENGLISH|Exercise SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)|16 VideosWORK, ENERGY AND POWER
AAKASH INSTITUTE ENGLISH|Exercise SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-I)|3 VideosWORK, ENERGY AND POWER
AAKASH INSTITUTE ENGLISH|Exercise SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)|60 VideosWAVES
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))|12 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-WORK, ENERGY AND POWER-SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
- A block of mass m is taken from A to B under the action of a constant ...
Text Solution
|
- A body of mas m starts from rest with a constant power. If velocity of...
Text Solution
|
- A body is moved from rest along a straight line by a machine deliverin...
Text Solution
|
- The potential energy of a particle of mass m is given by U=(1)/(2)kx^(...
Text Solution
|
- Figure shows a body A at the top of a frictionless hemispherical inver...
Text Solution
|
- A ball suspended by a thread swings in a vertical plane so that its ac...
Text Solution
|
- A car of mass m has an engine which can deliver constant power P.the m...
Text Solution
|
- A particle of mass 0.1 kg is subjected to a force which varies with di...
Text Solution
|
- A particle is moving in a verticalcircle such that the tensionin the s...
Text Solution
|
- A block of mass M is attached to the lower end of a verticle spring. T...
Text Solution
|
- The bob of pendulum is project with horizontal velocity of sqrt(3gf) I...
Text Solution
|
- A uniform chain of mass 4 kg and length 2 m overhangs a smooth table w...
Text Solution
|
- A particle of mass m, attached to the end of string of length l is rel...
Text Solution
|
- A system consists of t wo identical masses A and B of mass m each conn...
Text Solution
|
- A car starts from rest and moves on a surface in which the coefficient...
Text Solution
|
- A particle falls from rest under gravity. Its potential energy with re...
Text Solution
|
- A particle of mass m is moving in a horizontal circle of radius r, und...
Text Solution
|
- A particle is placed on the top of a hemispherical shell of same mass....
Text Solution
|
- A bob is tied up with a string AB of length l. End A of the string is ...
Text Solution
|
- If the linear momentum is increased by 50%, then kinetic energy will b...
Text Solution
|