Text Solution
Verified by Experts
Topper's Solved these Questions
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section - J) Aakash Challengers Questions|13 VideosSYSTEM OF PARTICLES AND ROTATIONAL MOTION
AAKASH INSTITUTE ENGLISH|Exercise Try Yourself|63 VideosSYSTEM OF PARTICLES AND ROTATIONAL MOTION
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section - H) Multiple True-False Type Questions|4 VideosSEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section-D (Assertion and reason))|5 VideosTEST 1
AAKASH INSTITUTE ENGLISH|Exercise EXERCISE|21 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-SYSTEM OF PARTICLES AND ROTATIONAL MOTION-Assignment (Section - I) Subjective Type Questions
- Figure shows a right angled triangle of uniform mass per unit area, at...
Text Solution
|
- A particle of mass m is moving anticlockwise, in a circle of radius R ...
Text Solution
|
- Two blocks A and B of masses m and 2m are placed on a smooth horizonta...
Text Solution
|
- A ball is projected from ground with a speed 70m//s at an angle 45^(@)...
Text Solution
|
- A collar B of mass m is at rest and when it is in the position shown, ...
Text Solution
|
- A uniform disc (of mass M and radius a) has a hole (of radius b) drill...
Text Solution
|
- A billiard ball, initially at rest, is given a sharp impulse by a cue....
Text Solution
|
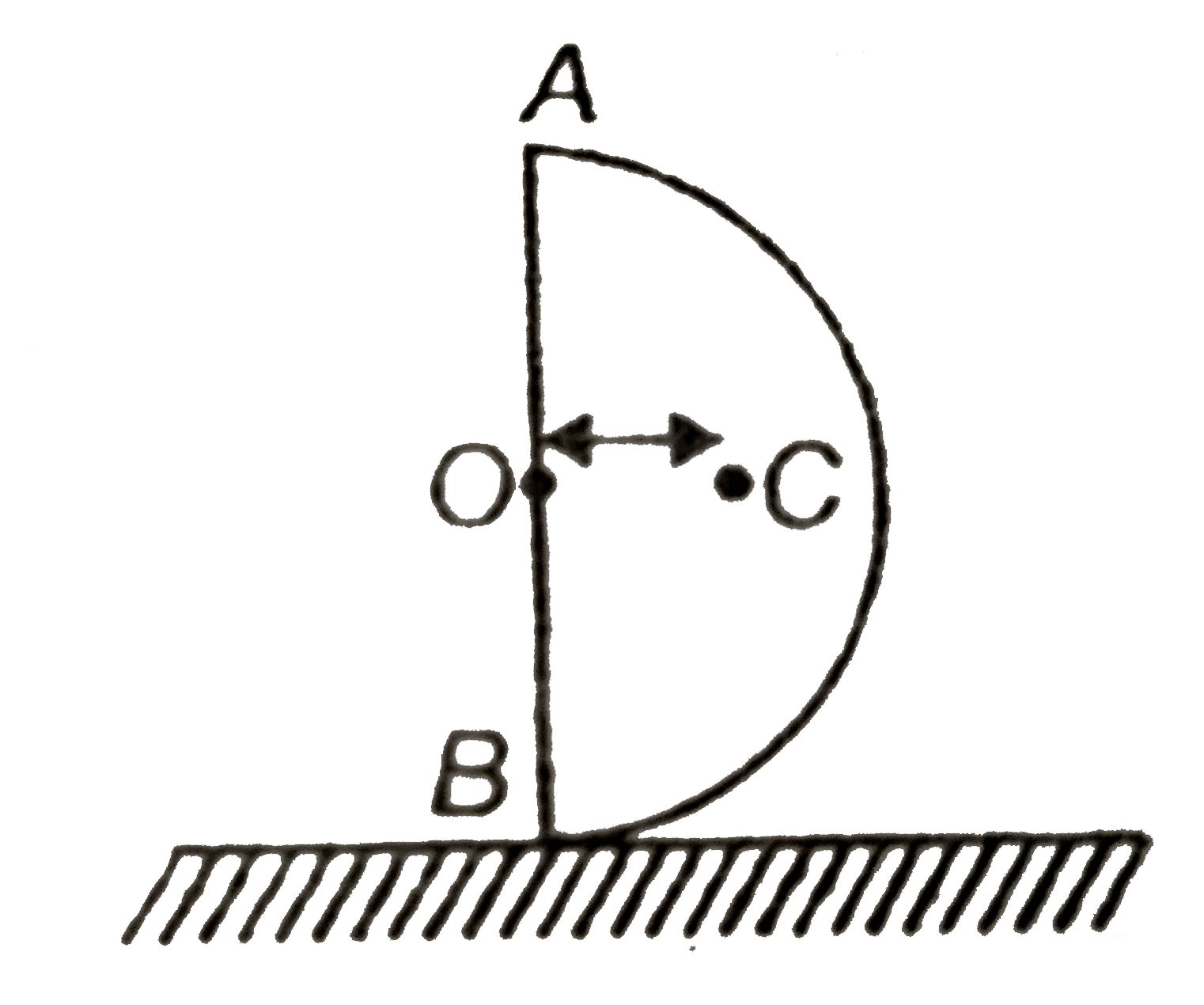
- A semicircle disc of mass M and radius R is held on a rough horizontal...
Text Solution
|