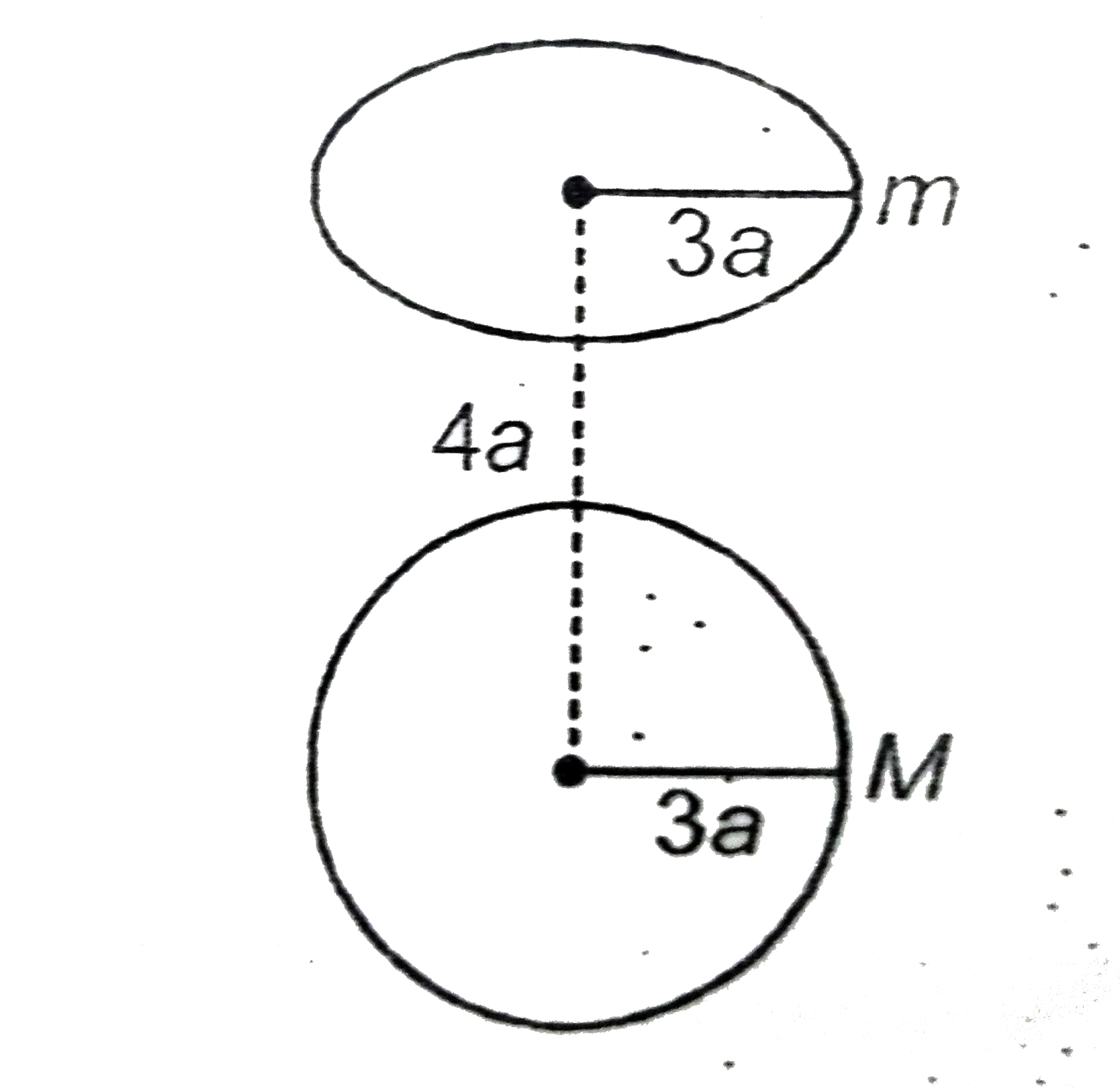Text Solution
Verified by Experts
Topper's Solved these Questions
GRAVITATION
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT SECTION -J (Aakash Challengers Questions)|6 VideosGRAVITATION
AAKASH INSTITUTE ENGLISH|Exercise TRY YOUR SELF|33 VideosGRAVITATION
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT SECTION -H (Multiple True - False Type Questions)|5 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT SECTION - D|9 VideosKINETIC THEORY
AAKASH INSTITUTE ENGLISH|Exercise EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions|10 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-GRAVITATION -ASSIGNMENT SECTION -I (Subjective Type Question)
- With what minimum velocity v should a particle be thrown horizontally ...
Text Solution
|
- A fixed spherical shell of inner radius R and outer radius 2R has mass...
Text Solution
|
- A uniform ring of mass m and radius 3a is kept above a sphere of mass ...
Text Solution
|
- A sphere of radius 2R and mas M has a spherical cavity of radius R as ...
Text Solution
|
- A point particle of mass m is released from a distance sqrt(3)R along ...
Text Solution
|
- A body is projected vartically upwards from the bottom of a crater of ...
Text Solution
|
- Two point particles of mass m and 2m are initially separated by a dist...
Text Solution
|
- An artificial satellite of mass m is given some kinetic at the surface...
Text Solution
|
- The distance between the centres of the Moon and the earth is D. The m...
Text Solution
|