Home
Class 12
PHYSICS
Calculate the rate of flow of glycerine ...

Calculate the rate of flow of glycerine of density 1.20 `xx 10^(3) kg//m^(3)` through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 `N/m^(2)`.

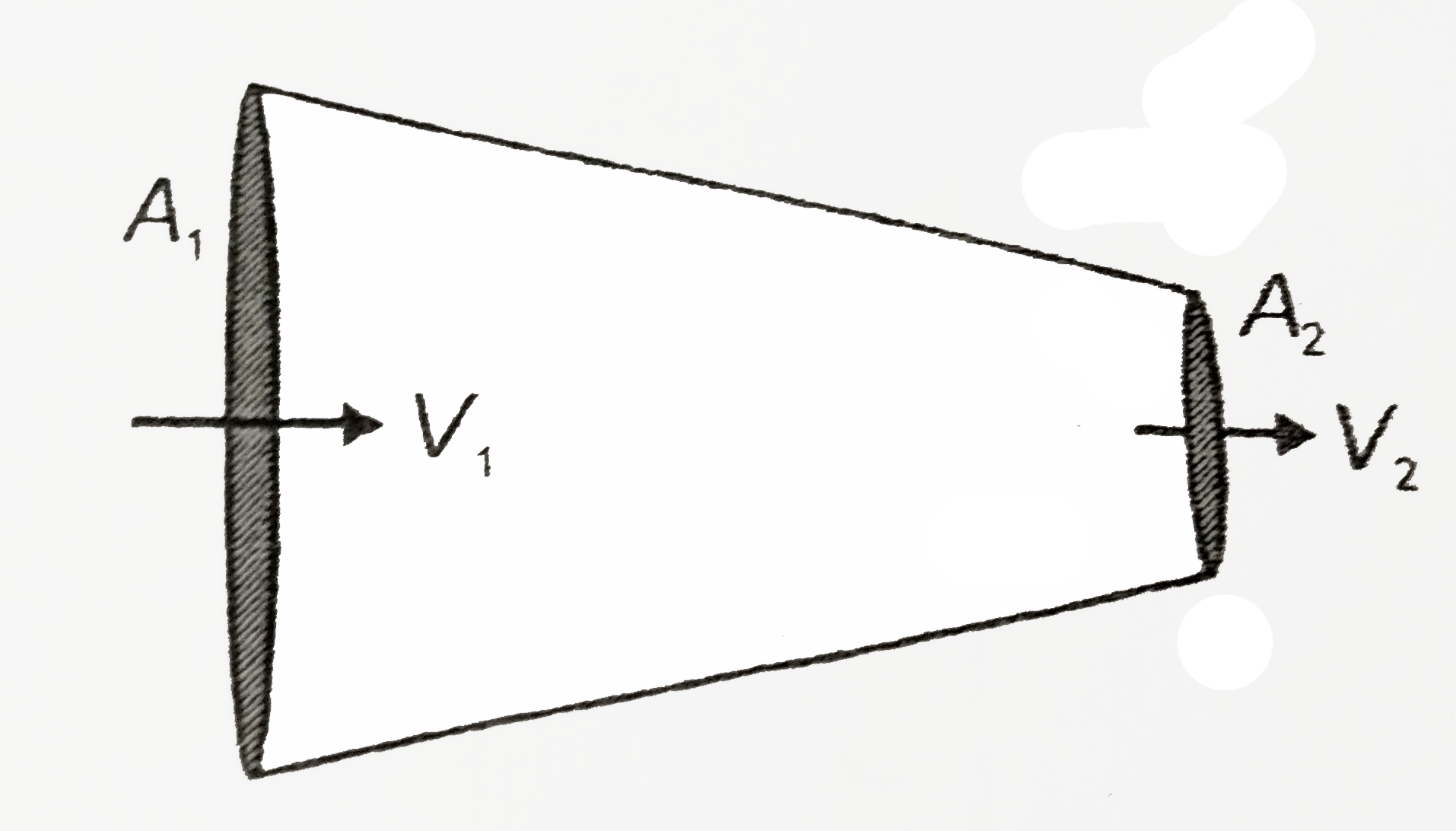
Text Solution

Verified by Experts

According to continuity equation,
`A_(1)V_(1) = A_(2)V_(2)`
`rArr (V_(2))/(V_(1))=(A_(1))/(A_(2))=(pi r_(1)^(2))/(pi r_(2)^(2))=(r_(1)^(2))/(r_(2)^(2))`
`rArr (V_(2))/(V_(1))=((r_(1))/(r_(2)))^(2)=((0.10)/(0.02))^(2)=5^(2)=25" "...(i)`
and according to Bernoulli's equation
`P_(1)+(1)/(2)rho v_(1)^(2)+rho gh_(1)=P_(2)+(1)/(2)rho v_(2)^(2)+rho gh_(2)`
Here pipe is horizontal. So `h_(1) = h_(2)`
`rArr P_(1)+(1)/(2) rho v_(1)^(2) + rho gh_(1) = P_(2) + (1)/(2)rho v_(2)^(2) + rho gh_(1)`
`rArr P_(1) + (1)/(2) rho v_(1)^(2)=P_(2)+(1)/(2)rho v_(2)^(2)`
`rArr (1)/(2) rho v_(2)^(2) - (1)/(2) rho v_(1)^(2) = P_(1)-P_(2)`
`rArr v_(2)^(2)-v_(1)^(2)=(2(P_(1)P_(2)))/(rho)=(2xx10)/(1.20 xx 10^(3))=(20)/(1.20 xx 10^(3))`
`rArr v_(2)^(2) - v_(1)^(2) = (20)/(1200) = (2)/(120) = (1)/(60) = 16.7 xx 10^(-3)" "...(ii)`
Substituting the value of `V_(2)` from equation (i) in (ii)
`(25 V_(1))^(2) - V_(1)^(2) = 16.7 xx 10^(-3)`
`rArr 624 V_(1)^(2) = 16.7 xx 10^(-3)`
`rArr v_(1)^(2) = (167 xx 10^(-4))/(624)`
`rArr V_(1) = sqrt((167)/(624))xx 10^(-2)m//sec`
So, rate of flow through the tube
`R=A_(1)V_(1)=A_(2)V_(2) = pi xx (0.1)^(2) xx sqrt((167)/(624)) xx 10^(-2)`
`=pi xx sqrt((167)/(624))xx 10^(-4)`
Promotional Banner

Topper's Solved these Questions

  • MECHANICAL PROPERTIES OF FLUIDS

    AAKASH INSTITUTE ENGLISH|Exercise TRY YOURSELF|41 Videos

  • MECHANICAL PROPERTIES OF FLUIDS

    AAKASH INSTITUTE ENGLISH|Exercise SECTION - A|50 Videos

  • MAGNETISM AND MATTER

    AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (SECTION D)|26 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    AAKASH INSTITUTE ENGLISH|Exercise Assignment(Section-D)|14 Videos

Similar Questions

Explore conceptually related problems

Calculate the rate of flow of glycerine of density 1.25xx10^(3) kg m^(-3) through the conical section of a pipe, if the radii of its ends are 0.1 m and 0.04 m and the pressure drop across its length is 10 Nm^(-2) .

In the figure shown below, a fluid of density 2 xx 10^(3) kg m^(-3) is flowing in a horizontal pipe. The speed of water at point A is 4 cm s^(-1) , what is its speed at point B?

Calculate the pH of 1.0xx10^(3) M solution of NaCI

A wire of density 9 xx 10^(3) kg//m^(3) is stretched between two clamps 1m apart and is stretched to an extension of 4.9 xx 10^(-4) m . Young's modulus of material is 9 xx 10^(10) N//m^(2) .

To what height does a liquid of density 0.4 xx 10^(3) kg m^(-3) and surface tension 0.05 Nm^(-1) rise in a capillary tube of radius 0.2 mm when dipped in ? [Given cos theta = 0.4 g = 10 m s^(-2) ]

The volume of a cuboid is 7. 68 m ^(3) if its length = 3.2 m and height = 1.0 m find its breadth.

Two metal spheres are falling through a liquid of density 2xx10^(3)kg//m^(3) with the same uniform speed. The material density of sphere 1 and sphere 2 are 8xx10^(3)kg//m^(3) and 11xx10^(3)kg//m^(3) respectively. The ratio of their radii is :-

The volume of a cuboid is 7.68 m ^(3) if its length =3.2 m and height = 1.0 m : find its breadth.

An oil drop of diameter 4 xx 10^(-6) m falls through air. iF the densities of the oil and air are 900 kg/m^(3) and 1.293 kg/m^(3) respectively and the coefficient of viscosity of air is 2.0 xx 10^(-5) Ns//m^(2) , then the terminal velocity of oil drop will be

Calculate the speed of a transverse wave in a wire of 1.0 mm^(2) cross-section under a tension of 0.98 N . Density of the material of wire is 9.8 xx 10^(3) kg//m^(3)