Text Solution
Verified by Experts
Topper's Solved these Questions
MOVING CHARGES AND MAGNETISM
AAKASH INSTITUTE ENGLISH|Exercise Illustration|14 VideosMOVING CHARGES AND MAGNETISM
AAKASH INSTITUTE ENGLISH|Exercise Try Yourself|27 VideosMOVING CHARGE AND MAGNESIUM
AAKASH INSTITUTE ENGLISH|Exercise SECTION D|16 VideosNUCLEI
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (SECTION-D)|10 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-MOVING CHARGES AND MAGNETISM-Assignment Section J (Aakash Challengers Questions)
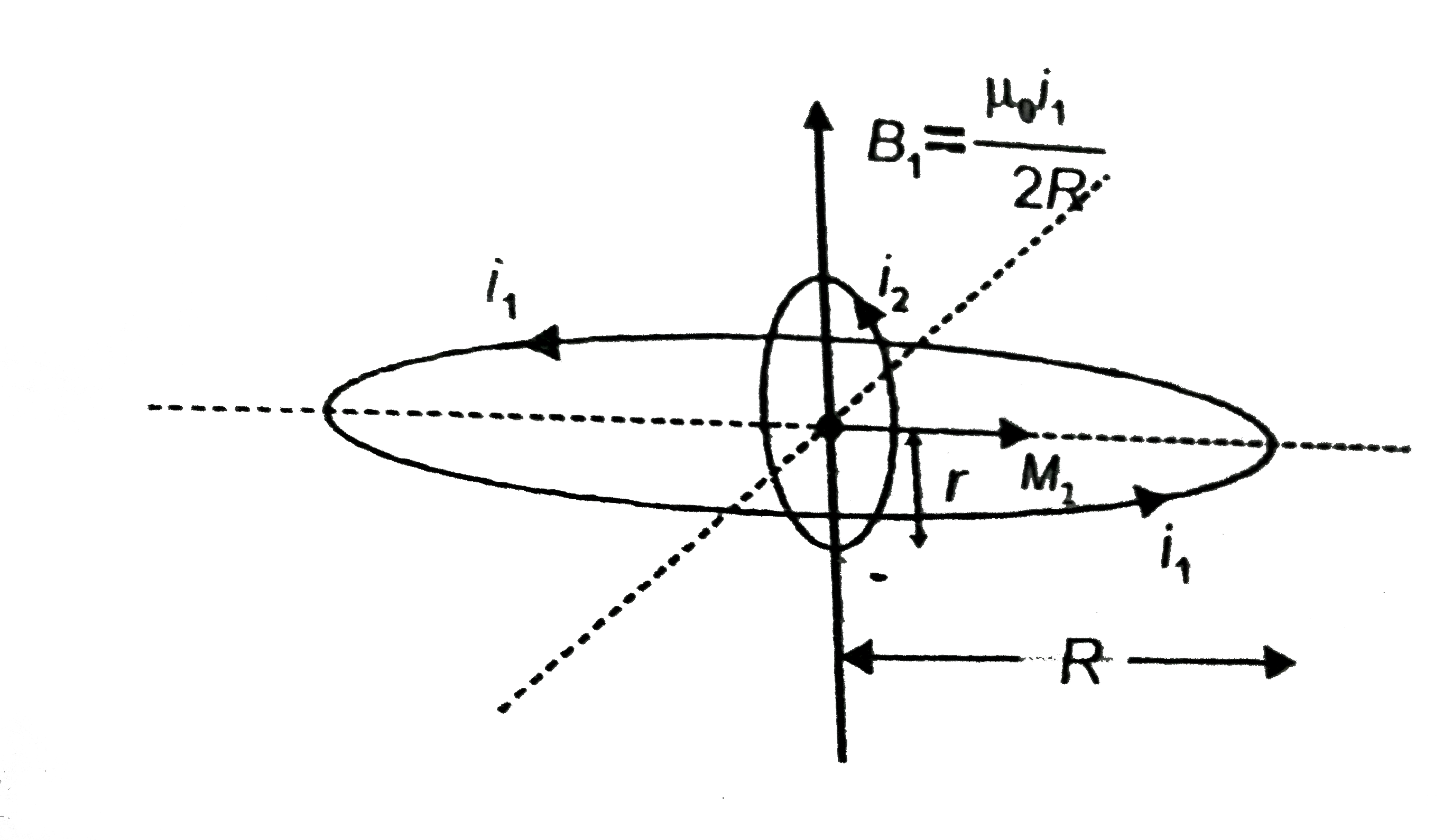
- A coil of radius R carries a current i(1). Another concentric coil of ...
Text Solution
|
- A long straight copper wire, of circular cross ection, contains n cond...
Text Solution
|
- Two coaxial plane coils, each of n turns of radius a, are separated by...
Text Solution
|
- State the Biot-Savart law which gives the magnetic field B at a distan...
Text Solution
|
- In a helium dilution refrigerator .^(3)He and .^(4)He are mixed in a s...
Text Solution
|
- Two long concetric cylindrical conductors of radii a and b (b lt a) ar...
Text Solution
|