Text Solution
Verified by Experts
Topper's Solved these Questions
RAY OPTICS AND OPTICAL INSTRUMENTS
AAKASH INSTITUTE ENGLISH|Exercise EXAMPLE|75 VideosRAY OPTICS AND OPTICAL INSTRUMENTS
AAKASH INSTITUTE ENGLISH|Exercise EXERCISE|45 VideosRAY OPTICS AND OPTICAL INSTRUMENTS
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section - I) Subjective Type Questions|6 VideosPHYSICAL WORLD
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (Section-B)|4 VideosSEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )
AAKASH INSTITUTE ENGLISH|Exercise Assignment SECTION - D (Assertion & reason type Question)|10 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-RAY OPTICS AND OPTICAL INSTRUMENTS-Assignment (Section - J) Aakash Challengers Questions
- A particle is projected from a horizontal floor with speed 10(m)/(s) a...
Text Solution
|
- A ball is kept at a height h above the surface of a heavy transparent ...
Text Solution
|
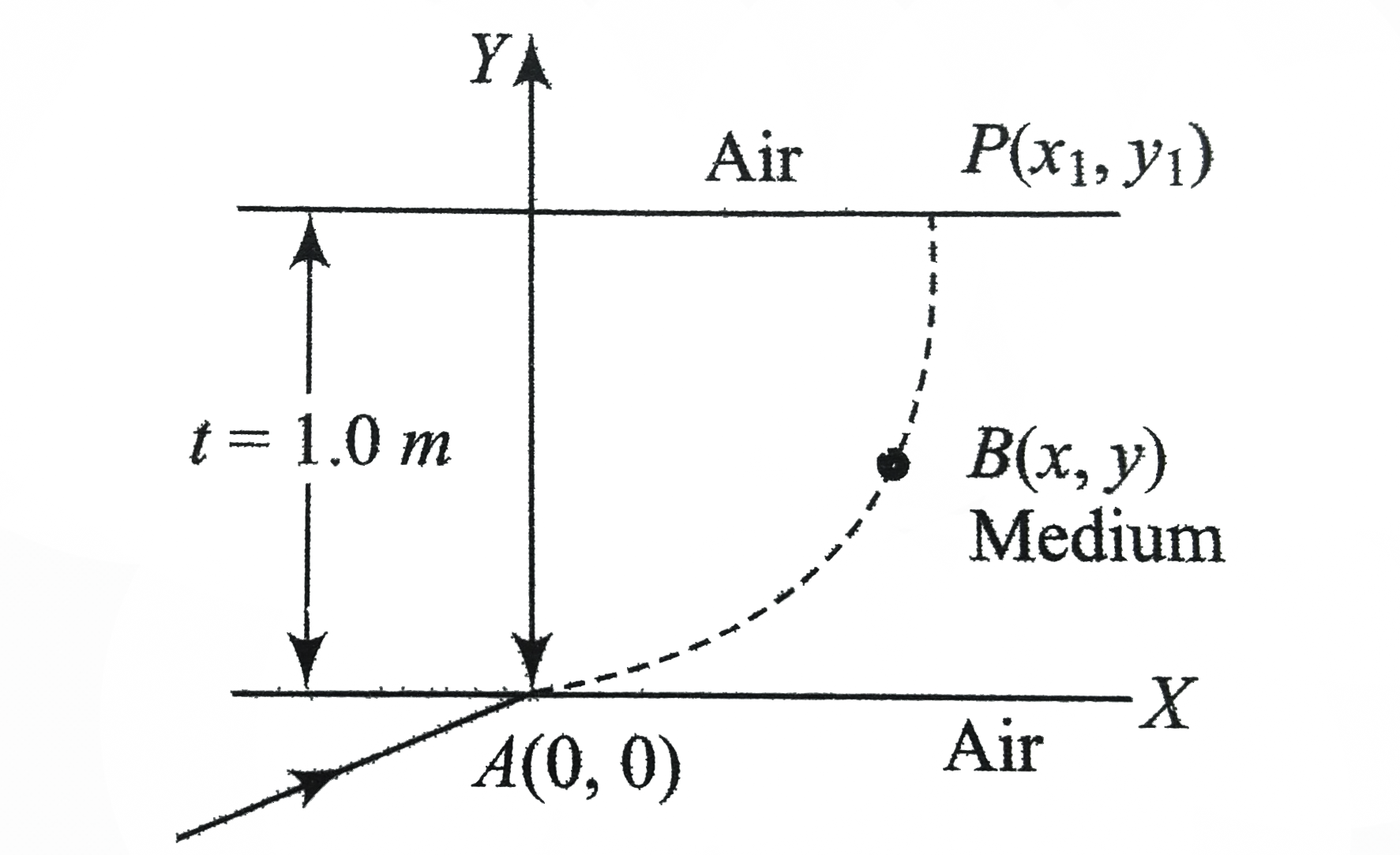
- A ray of light travelling in air in inciden tat grazing angle (inciden...
Text Solution
|
- Does the escape speed of a body from the earth depend on. (i)mass of...
Text Solution
|
- A particle executes a simple harmonic motion of amplitude 1.0 cm along...
Text Solution
|
- The refractive index of the crown glass for violet and red lights are ...
Text Solution
|
- A satellite is launched into a circular orbit of radius R around the e...
Text Solution
|