Home
Class 12
PHYSICS
A particle of mass is confined to a narr...

A particle of mass is confined to a narrow tube of length L.
(a) Find the wavelengths of the de-Brogile wave which will resonate in the tube.
(b) Calculate the corresponding particle moments. and
(c) Calculate the corresponding energies.

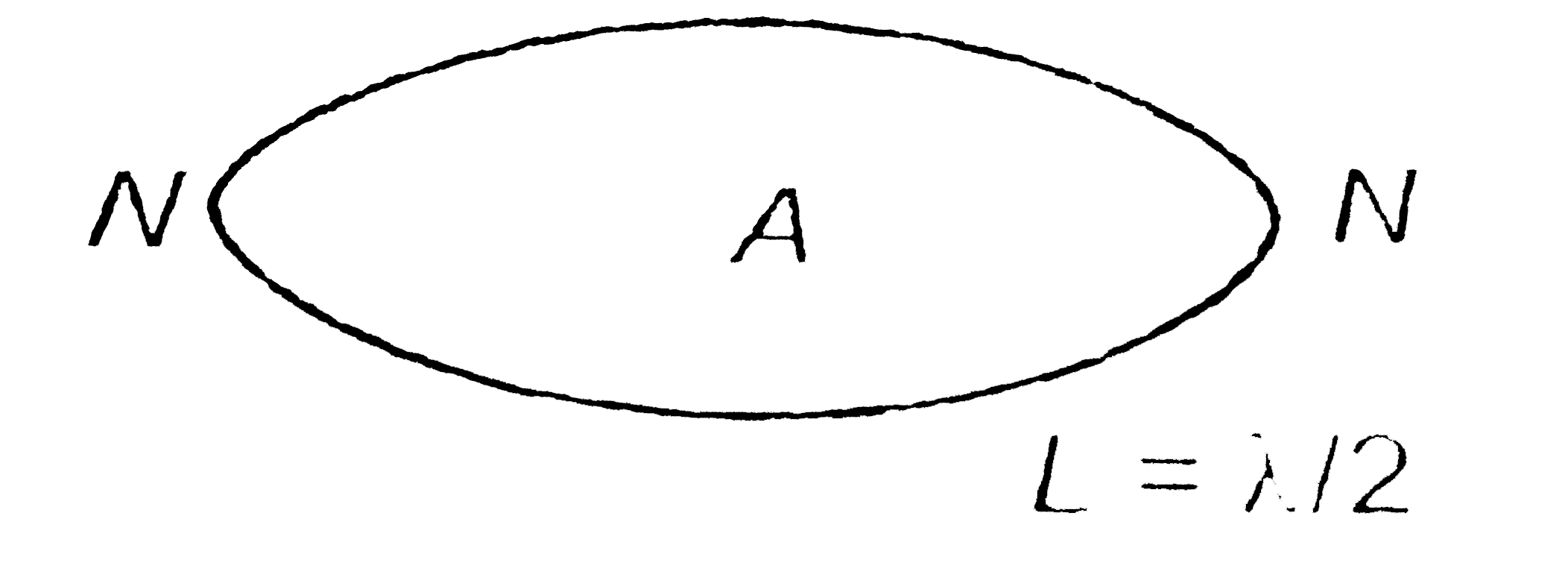
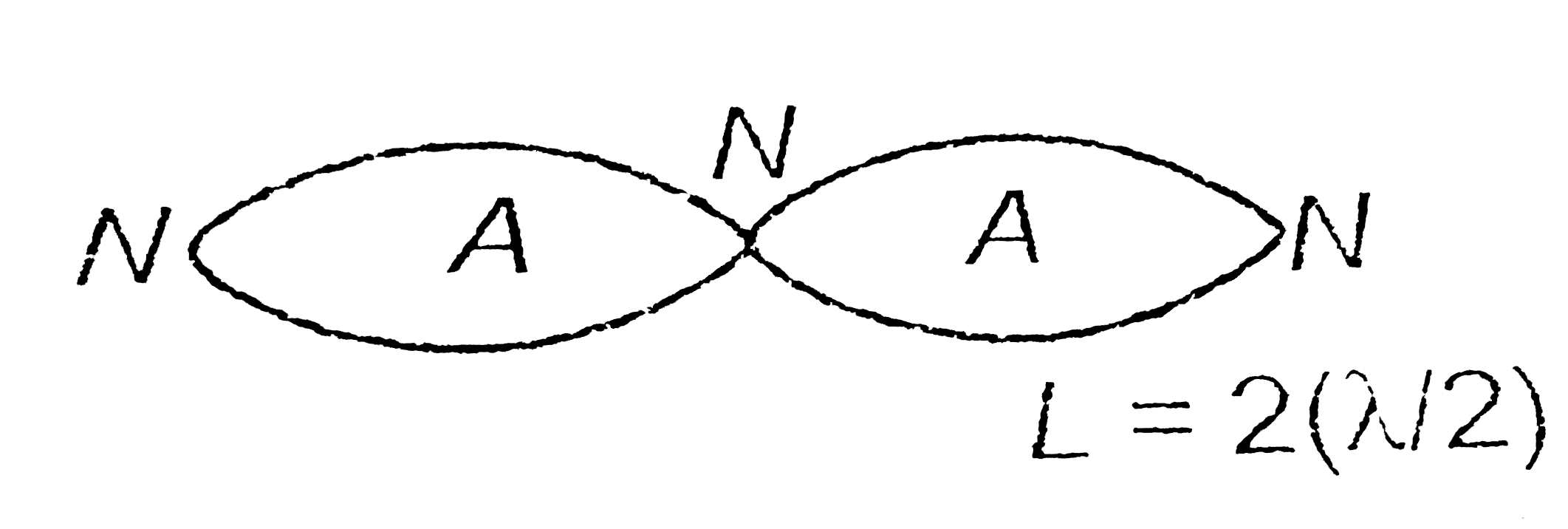
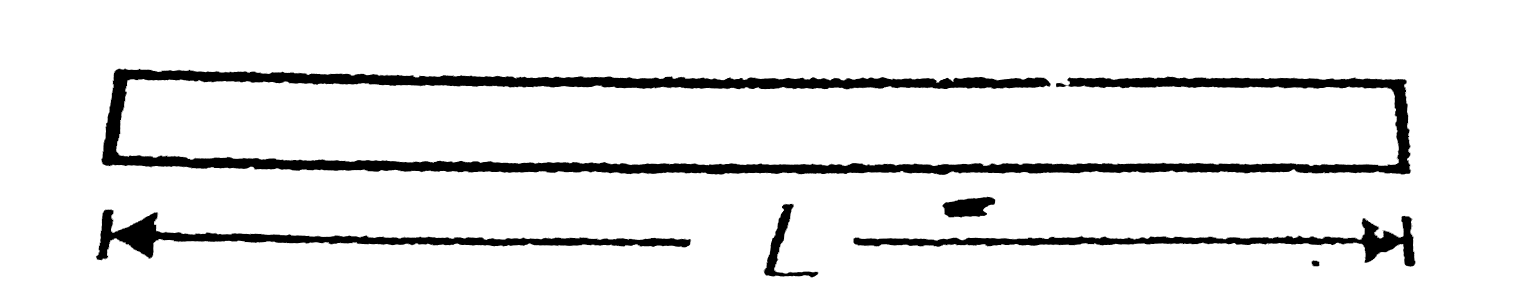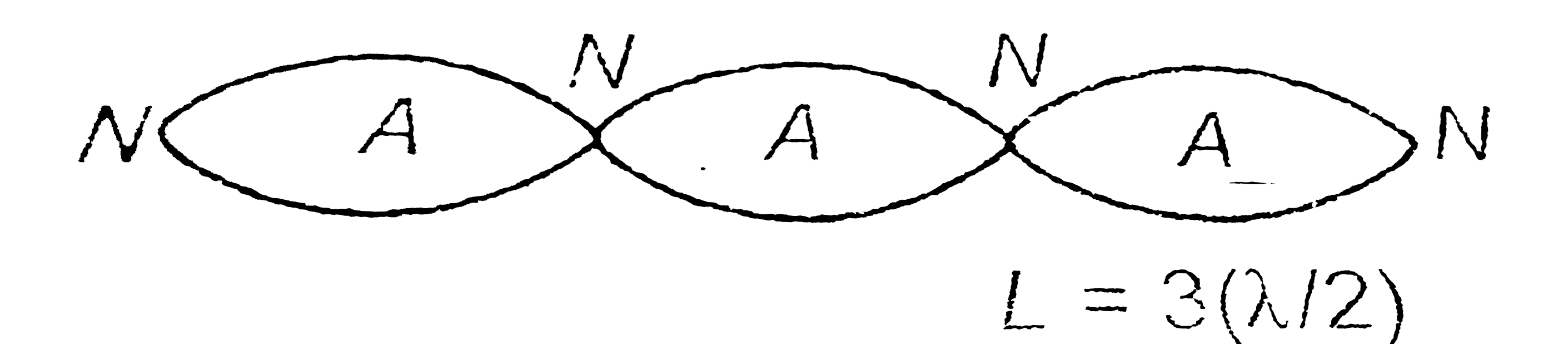Text Solution

Verified by Experts

(a)The de-Broglie waves will resonate with a node at each end of the tube.

A few of the possible resonance forms are as follows :
`lambda_n="2L"/n, n=1,2,3`……

(b)Since de-Broglie wavelengths are `lambda_n=h/p_n`
`p_n=h/lambda_n`
`="nh"/"2L"`, n=1,2,...

(c ) The kinetic energy of the particles are `K_n=p_n^2/"2m"`

`=(n^2h^2)/(8L^2m) n=1,2,3`......
Promotional Banner

Topper's Solved these Questions

  • ATOMS

    AAKASH INSTITUTE ENGLISH|Exercise Try Yourself|24 Videos

  • ATOMS

    AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT SECTION A Objective (One option is correct )|35 Videos

  • ALTERNATING CURRENT

    AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section-J) (Aakash Chailengers Questions)|2 Videos

  • COMMUNICATION SYSTEMS

    AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT SECTION D (Assertion-Reason)|10 Videos

Similar Questions

Explore conceptually related problems

A material particle with a rest mass m_o is moving with a velocity of light c. Then, the wavelength of the de Broglie wave associated with it is

wavelength of Bullet. Calculate the de-Brogli wavelength of a 5.00 g bullet that is moving at 340 m/s will it exhibite wave like particle?

Calculate the momentum of a particle which has de Broglie wavelength of 0.1 nm.

A particle is moving three times as fast as an electron. The ratio of the de- Broglie wavelength of the particle to that of the electron is 1.813xx10^-4 . Calculate the particle's mass and identify the particle. Mass of electron =9.11xx10^(-31)kg .

A particle is moving three times as fast as an electron. The ratio of the de- Broglie wavelength of the particle to that of the electron is 1.813xx10^-4 . Calculate the particle's mass and identify the particle. Mass of electron =9.11xx10^(-31)kg .

A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.

A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.

When a particle is restricted to move along x-axis between x=0 and x=a , where alpha if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a . The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=(p^2)/(2m) . Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...( n=1 , called the ground state) corresponding to the number of loops in the standing wave. Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=alpha . Take h=6.6xx10^(-34)Js and e=1.6xx10^(-19) C. Q. If the mass of the particle is m=1.0xx10^(-30) kg and alpha=6.6nm , the energy of the particle in its ground state is closest to

When a particle is restricted to move along x-axis between x=0 and x=a , where alpha if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a . The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=(p^2)/(2m) . Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...( n=1 , called the ground state) corresponding to the number of loops in the standing wave. Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=alpha . Take h=6.6xx10^(-34)Js and e=1.6xx10^(-19) C. Q. The allowed energy for the particle for a particular value of n is proportional to

When a particle is restricted to move along x-axis between x=0 and x=a , where alpha if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a . The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=(p^2)/(2m) . Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...( n=1 , called the ground state) corresponding to the number of loops in the standing wave. Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=alpha . Take h=6.6xx10^(-34)Js and e=1.6xx10^(-19) C Q. The speed of the particle that can take discrete values is proportional to