Text Solution
Verified by Experts
Topper's Solved these Questions
INVERSE TRIGONOMETRIC FUNCTIONS
AAKASH INSTITUTE ENGLISH|Exercise TRY YOURSELF|21 VideosINVERSE TRIGONOMETRIC FUNCTIONS
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (SECTION - A)(OBJECTIVE TYPE QUESTIONS (ONE OPTION IS CORRECT))|45 VideosINTEGRALS
AAKASH INSTITUTE ENGLISH|Exercise Try yourself|50 VideosLIMITS AND DERIVATIVES
AAKASH INSTITUTE ENGLISH|Exercise Section - j|3 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-INVERSE TRIGONOMETRIC FUNCTIONS-ASSIGNMENT (SECTION - J)(ANKASH CHALLENGERS QUESTIONS)
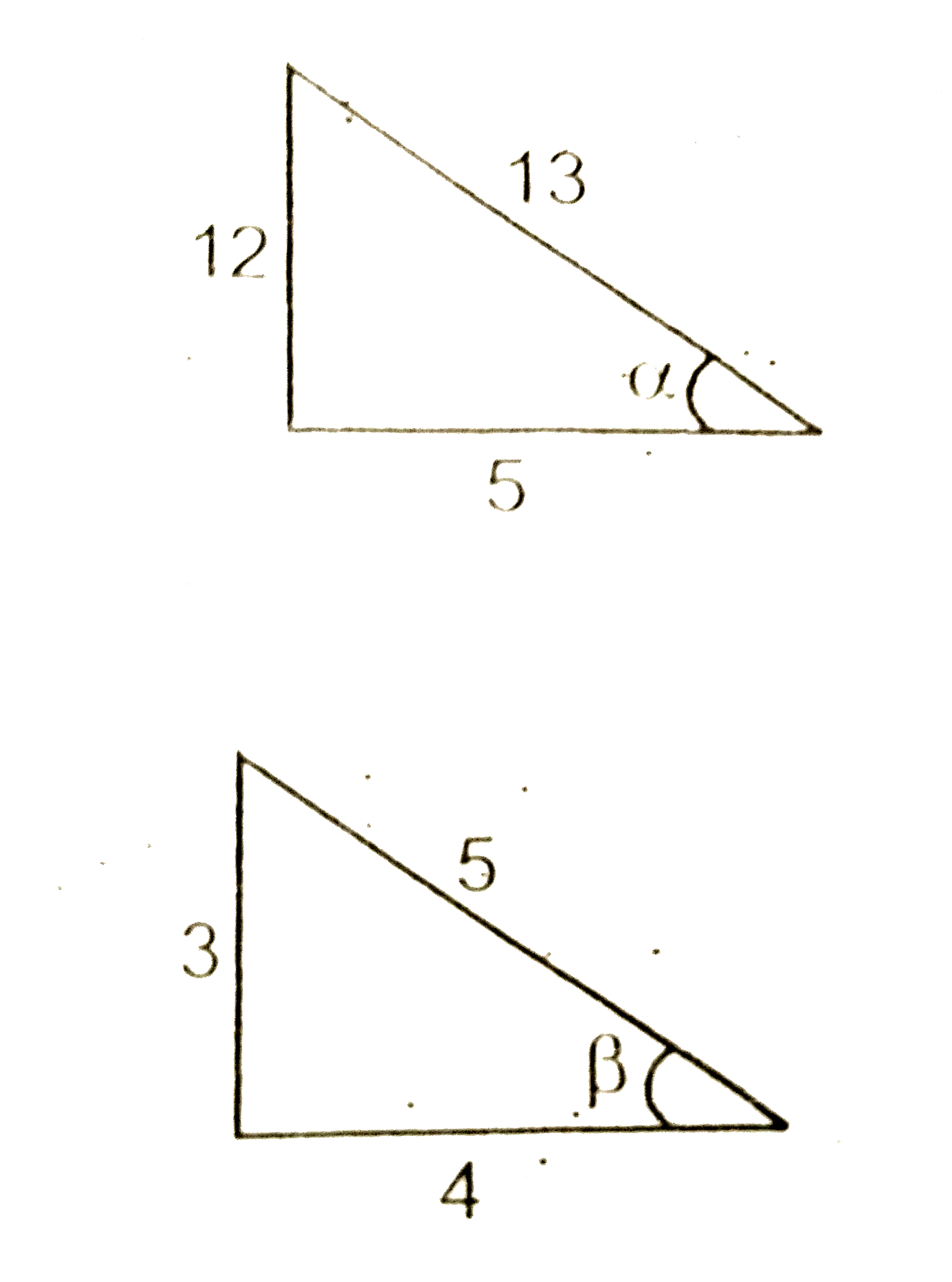
- Prove that: sin^(-1)(12)/(13)+cos^(-1)4/5+tan^(-1)(63)/(16)=pi
Text Solution
|
- The total number of solutions of the equation sin^-1(3/5 x)+sin^-1(4/5...
Text Solution
|
- The value (s) of theta satisfying the equation theta=tan^(- 1)(2tan^2t...
Text Solution
|
- Show that : 2\ tan^(-1){tanalpha/2tan(pi/4-beta/2)}=tan^(-1)((sinalpha...
Text Solution
|
- The total number of ordered pairs of (x,y) satisfying the equation 13+...
Text Solution
|