Home
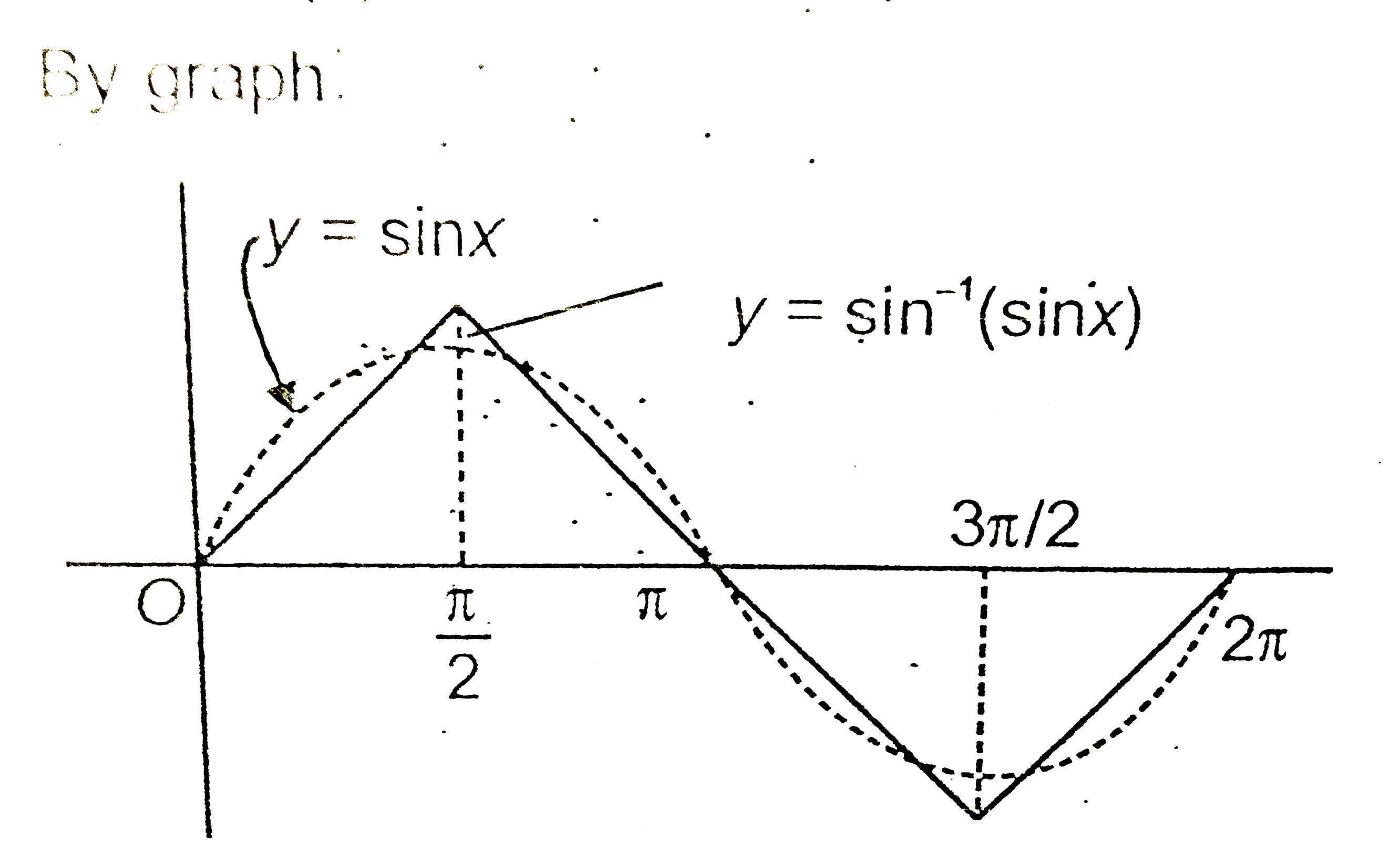
Class 12
MATHS
Solutions of sin^(-1) ( sin x) = sin x "...

Solutions of `sin^(-1) ( sin x) = sin x " are , if " x in ( 0, 2pi)`

A

4 real roots

B

2 positive real roots

C

2 negative real roots

D

5 real roots

Text Solution

Verified by Experts

The correct Answer is:
D
By graph

Option 4 is correct.
Promotional Banner

Topper's Solved these Questions

  • INVERSE TRIGONOMETRIC FUNCTIONS

    AAKASH INSTITUTE ENGLISH|Exercise TRY YOURSELF|21 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (SECTION - A)(OBJECTIVE TYPE QUESTIONS (ONE OPTION IS CORRECT))|45 Videos

  • INTEGRALS

    AAKASH INSTITUTE ENGLISH|Exercise Try yourself|50 Videos

  • LIMITS AND DERIVATIVES

    AAKASH INSTITUTE ENGLISH|Exercise Section - j|3 Videos

Similar Questions

Explore conceptually related problems

Solutions of sin^(-1) (sinx) = sinx are if x in (0, 2pi)

Solve sin^(-1) (sin 6x) = x, x in [0,pi]

Number of solutions of the equation 2 sin^3x + 6 sin^2x -sin x-3=0 in (0, 2pi), are

Find the solution set for , 4 sin^(2)x -8 sin x +3 le 0 where x in [0,2pi]

If y=sin^(-1)(sin x), then dy/dx at x =pi/2 is

The number of solutions of the equation sin x . Sin 2x. Sin 3x=1 in [0,2pi] is

Solve cos^(-1) (cos x) gt sin^(-1) (sin x), x in [0, 2pi]

Find the number of solutions of the equations (sin x - 1)^(3) + (cos x - 1)^(3) + ( sin x)^(3) = ( 2 sin x + cos x - 2)^(3) in ( 0, 2 pi) .

The solution of sin^(-1)|sin x|=sqrt(sin^(-1)|sin x|) is

The total number of solution of the equation sin^4 x +cos^4 x = sin x cos x in [0,2pi] is :