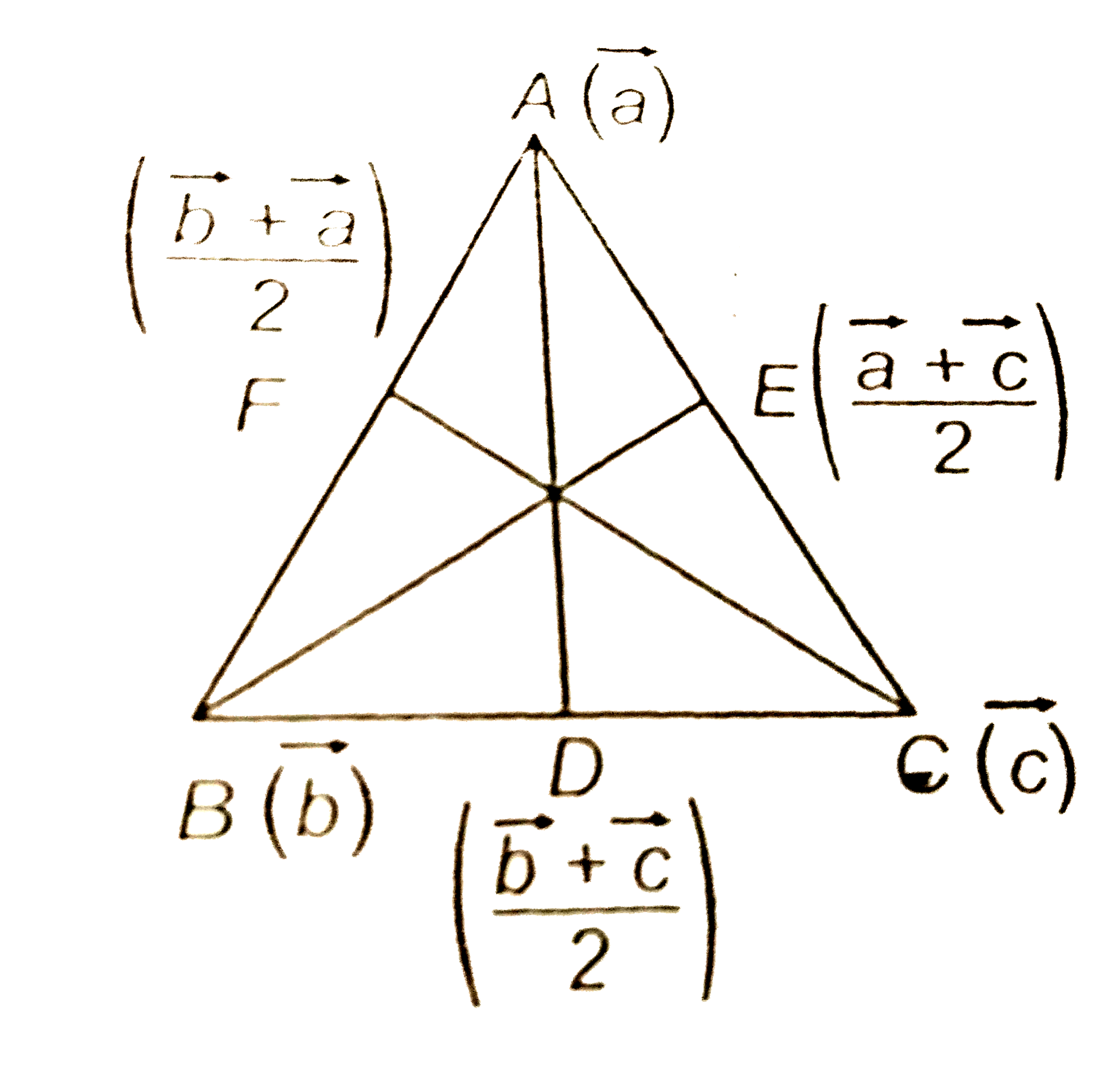Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-VECTOR ALGEBRA-SECTION-J (Aakash Challengers Questions)
- Prove using vectors: Medians of a triangle are concurrent.
Text Solution
|
- Sholve the simultasneous vector equations for vecx and vecy: vecx+vecc...
Text Solution
|
- Let veca=a(1)hati+a(2)hatj+a(3)hatk,vecb=b(1)hati+b(2)hatj+b(3)hatk an...
Text Solution
|
- If veca,vecb,vecc are non-coplanar vectors and vecu and vecv are any t...
Text Solution
|
- If |{:(p,p^(2),1+p^(3)),(q,p^(2),1+q^(3)),(r,r^(2),1+r^(3)):}|=0 and t...
Text Solution
|
- If veca,vecb,vecc are mutually perpendicular vectors of equal magnitud...
Text Solution
|