Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
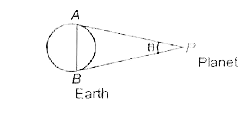
- The parallax of a far off planet as measured from the two diametric ex...
Text Solution
|
- The mass of a planet is six times that of the earth. The radius of the...
Text Solution
|
- The parallax of a heavenly body measured from tow points diametrically...
Text Solution
|
- The moon subtends an angle of 57 minutes at the base line equal to rad...
Text Solution
|
- The moon is observed from two diametrically extremes A and B on earth....
Text Solution
|
- A far off planet is estimated to be at a distance D from the earth. If...
Text Solution
|
- पृथ्वी पर दो व्यासतः विपरीत स्थित बिंदुओं से एक खगोलीय पिंड क...
Text Solution
|
- पृथ्वी के व्यास के सिरों के बिंदुओं से किसी आकाशीय पिंड का लंबन कोण 2...
Text Solution
|
- पृथ्वी की दो व्यासतः अभिमुख (Diametrically opposite ) बिंदुओं से किसी...
Text Solution
|