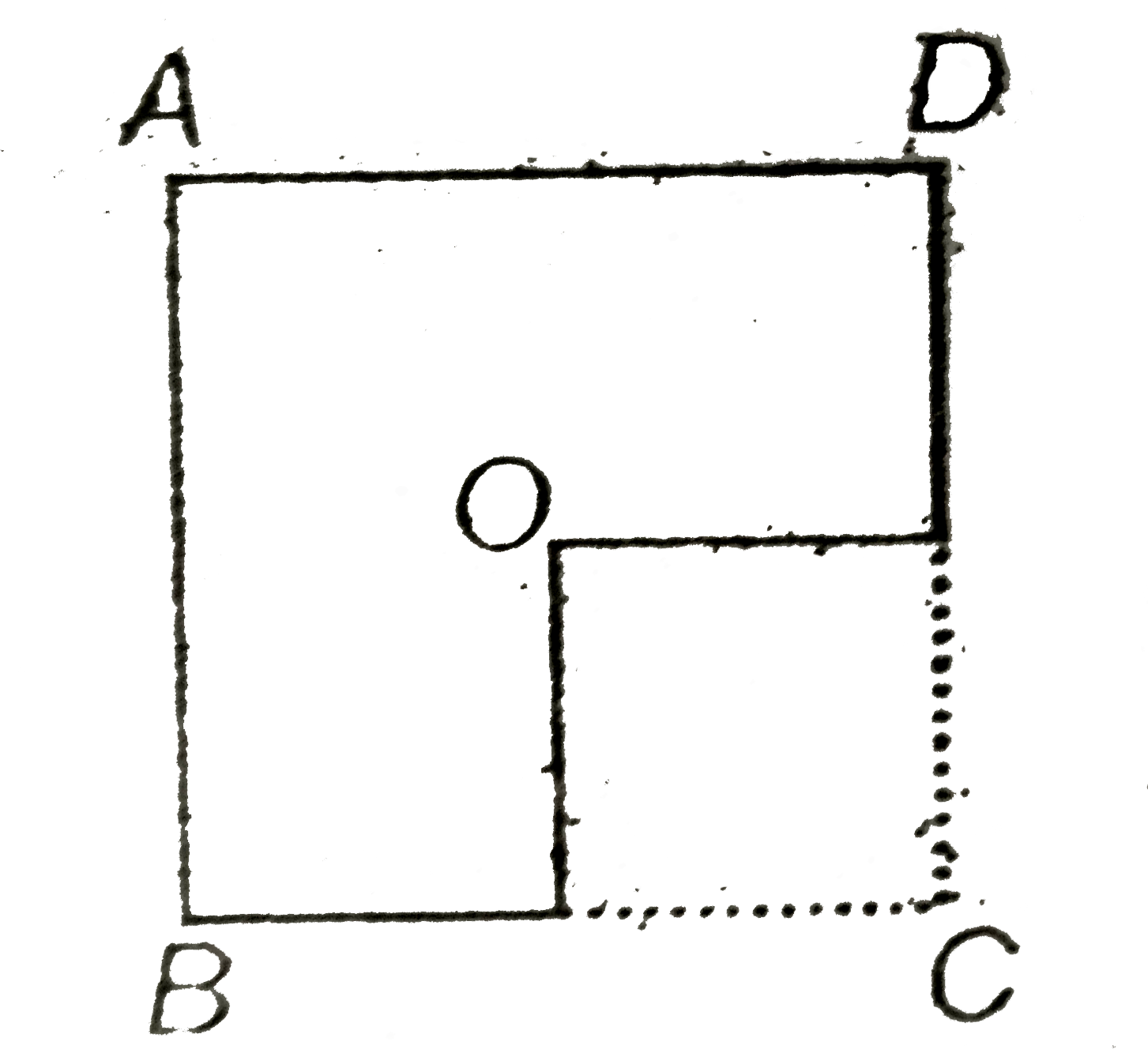
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- From a uniform square plate, one-fourth part is removed as shown. The ...
Text Solution
|
- A circular plate of unifrom thickness has a diameter of 56 cm. A circu...
Text Solution
|
- A square of side a and uniform thickness is divided into four equal pa...
Text Solution
|
- In the figure shown a semicircular area is removed from a uniform squa...
Text Solution
|
- Figure shows a square plate of uniform thickness and side length sqrt ...
Text Solution
|
- From a uniform square plate the shaped portions are removed as shown i...
Text Solution
|
- In the figure one fourth part of a uniform disc of radius R is shown. ...
Text Solution
|
- Fron a sqaure plate of side a,a quarter circular disc of radius a is r...
Text Solution
|
- From a uniform square plate, one-fourth part is removed as shown. The ...
Text Solution
|