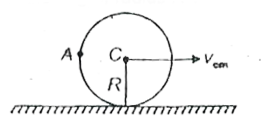
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In case of pure rolling what will be velocity of point A of the ring o...
Text Solution
|
- A disc of radius R is rolling purely on a flat horizontal surface, wit...
Text Solution
|
- A uniform ring of radius R is given a back spin of angular velocity V(...
Text Solution
|
- A ring of radius R is rolling purely on the outer surface of a pipe of...
Text Solution
|
- In figure-5.54 a wire ring of radius R is in pure rolling on a surface...
Text Solution
|
- In case of pure rolling, what will be the velocity of point A of the r...
Text Solution
|
- किसी लुढ़कते हुए छल्ले की सम्पूर्ण गतिज ऊर्जा ज्ञात कीजिए, यदि छल्ले का...
Text Solution
|
- In case of pure rolling what will be velocity of point A of the ring o...
Text Solution
|
- In pure rolling, the velocity at the point of contact:
Text Solution
|