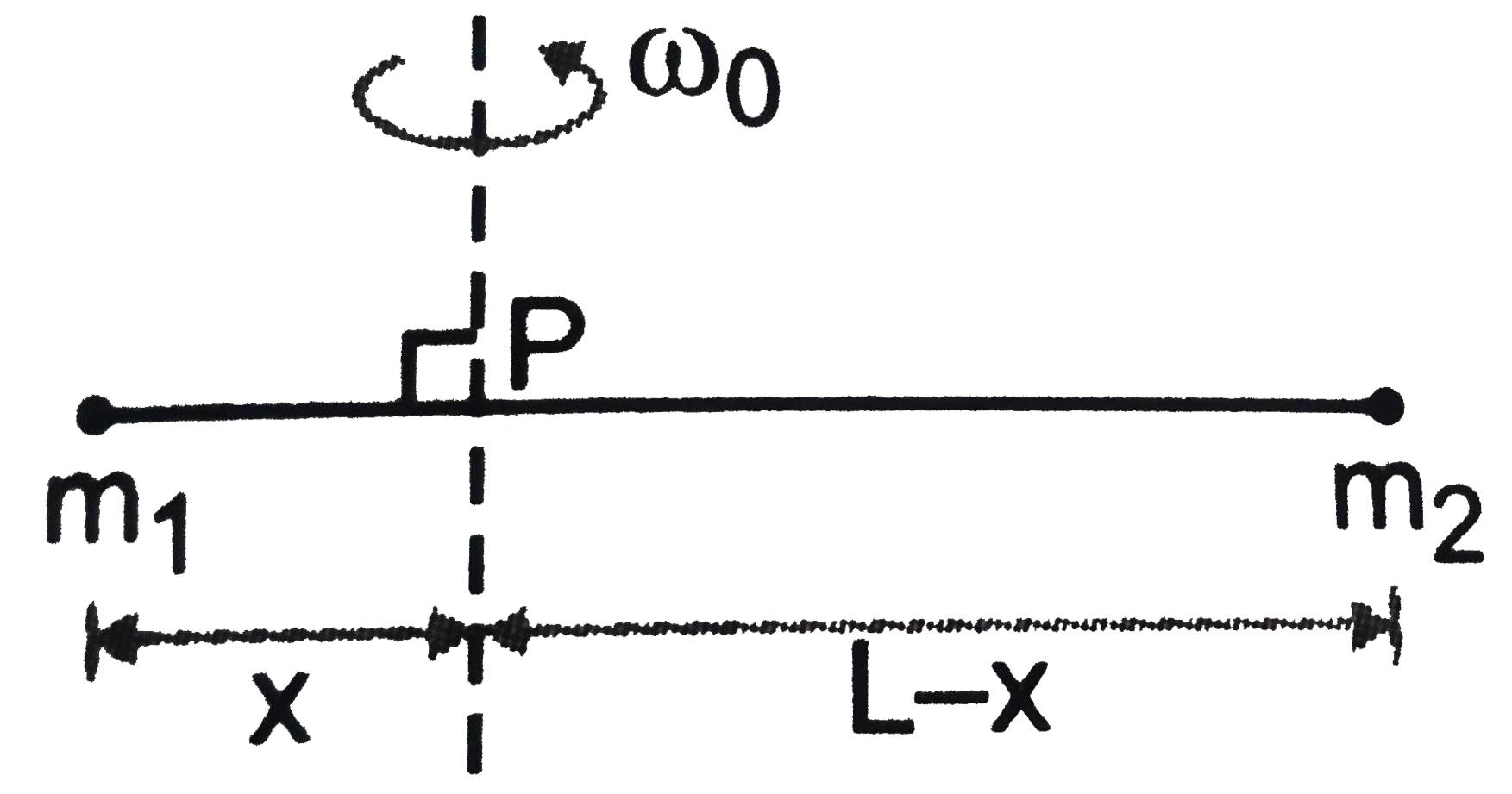
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Point masses m(1) and m(2) are placed at the opposite ends of a rigid ...
Text Solution
|
- Two point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of...
Text Solution
|
- A uniform rod of mass m is rotated about an axis passing through point...
Text Solution
|
- Point masses m(1) and m(2) are placed at the opposite ends of a rigid ...
Text Solution
|
- Two point masses A of mass M and B of mass of 4M are fixed at the ends...
Text Solution
|
- Point masses m(1) and m(2) are placed at the ends of a rigid rod of le...
Text Solution
|
- लम्बाई l की एक छड़ के सिरों पर बिंदु –द्रव्यमान M(1) तथा M(2) रखे हैं छ...
Text Solution
|
- एक हल्की छड़ की लम्बाई l है। इसके दो सिरों पर m(1) व m(2) द्रव्यमान के ...
Text Solution
|
- किसी दृढ़ छड़ की लम्बाई L है और इसका द्रव्यमान नगण्य है। इसके दो विपरील ...
Text Solution
|