A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
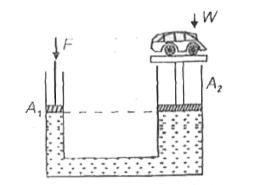
- In a hydraulic jack as shown, mass of the car is m = 800 kg,A(1) = 10 ...
Text Solution
|
- Let a(1),a(2),a(3),... be a G.P such that log(10)(a(m))=(1)/(n) and lo...
Text Solution
|
- The diameter of the piston of a hydraulic automobile is D metre. What ...
Text Solution
|
- An automobile sack is lifted by a hydraulic jack that consists of two ...
Text Solution
|
- The minimum mass of mixture of A(2) and B(2) required to produce at le...
Text Solution
|
- A car is lifted by a hydraulic jack that consists of two pistons. The ...
Text Solution
|
- For natural numbers m, n if (1-y)^(m)(1+y)^(n) = 1+a(1)y+a(2)y^(2) + "...
Text Solution
|
- In a hydraulic jack as shown, mass of the car is m = 800 kg,A(1) = 10 ...
Text Solution
|
- In car lift compressed air exerts a force F1 on a small piston having ...
Text Solution
|