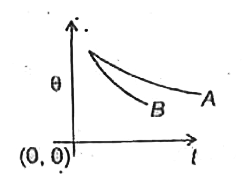
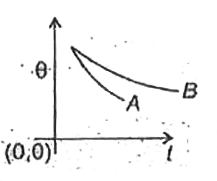
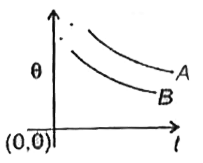
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two bodies A and B of same mass, area and surface finish with specific...
Text Solution
|
- Consider the following statements : S(1) : If A={a} and B = {a, b, c}...
Text Solution
|
- When sulphur ( in the form of S(B)) is heated at temperature T, at equ...
Text Solution
|
- Two identical spheres S(1) and S(2) out of which S(1) is placed on the...
Text Solution
|
- Equal masses of three liquids are thoroughly mixed. The specific heat ...
Text Solution
|
- The specific heat capacities of n liquid are s(1),s(2),s(3) ,…….. s(n)...
Text Solution
|
- "Two metallic spheres" S(1) "& "S(2) "area made of same material /Th...
Text Solution
|
- धातु के दो गोले S(1) व S(2) समान पदार्थ के बने है तथा दोनों की समरूप...
Text Solution
|
- Two bodies A and B of same mass, area and surface finish with specific...
Text Solution
|