Text Solution
Verified by Experts
Topper's Solved these Questions
OSCILLATIONS
AAKASH INSTITUTE ENGLISH|Exercise Exercise|18 VideosOSCILLATIONS
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)|60 VideosOSCILLATIONS
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT ( SECTION-J )|8 VideosNUCLEI
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (SECTION-D)|10 VideosPHYSICAL WORLD
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (Section-B)|4 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-OSCILLATIONS-EXAMPLE
- A nurse in a hospital , noted for a patient that heart was beating 75 ...
Text Solution
|
- Which of the following functions of time represented (a) periodic an...
Text Solution
|
- Categorise the following function of time : sin omega t + sin 3 omega ...
Text Solution
|
- Categories the following function of time 3 sin ( 2 omegat - (pi)/( 4)...
Text Solution
|
- Figure depicts two circular motions. The radius of the circle, the per...
Text Solution
|
- In the figure, dots and arrows show the position and the velocity of a...
Text Solution
|
- Plot the corresponding reference circle for given SHM, indicate the in...
Text Solution
|
- A particle executes a simple harmonic motion of time period T. Find th...
Text Solution
|
- A particle executes SHM with a time period of 2s and amplitude 10 cm ....
Text Solution
|
- A particle of mass 2 kg executing SHM has amplitude 10 cm and time pe...
Text Solution
|
- The speed of a particle executing SHM with amplitude of displacement 5...
Text Solution
|
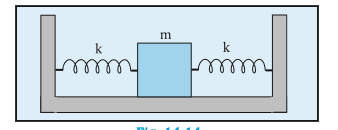
- Two identical springs of spring constant k are attached to a block of ...
Text Solution
|
- Howdoes the huge ball ( 5.4 xx 10^(5) kg ) hanging on the 22^(nd) floo...
Text Solution
|
- A block whose mass is 2 kg is fastened on a spring whose spring consta...
Text Solution
|
- A particle executes SHM with amplitude A and time period T. When the d...
Text Solution
|
- A particle of mass 0.2 kg is excuting SHM of amplitude 0.2 m. When it ...
Text Solution
|
- A 2.5 kg collar is attached to a spring of spring constant 250 Nm^(-...
Text Solution
|
- The length of the simple pendulum which ticks seconds is
Text Solution
|
- If the length of a simple pendulum of a clock incrreases by 2% how mu...
Text Solution
|
- For the damped oscillator shown in Figure, the mass m of the block is...
Text Solution
|