A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
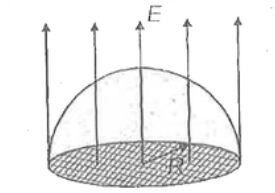
- A hemispherical surface of radius R is kept in a uniform electric fiel...
Text Solution
|
- A hemispherical body of radius R is placed in a uniform electric field...
Text Solution
|
- Find out the flux through the curved surface of a hemisphere of radius...
Text Solution
|
- The electric flux through a hemispherical surface of radius R placed i...
Text Solution
|
- A uniform field E is parallel to axis of a hollow hemisphere of radius...
Text Solution
|
- If a hemispherical body is placed in a uniform electric field E then t...
Text Solution
|
- A hemispherical body of radius R is placed in a uniform electric field...
Text Solution
|
- If a hemispherical body is placed in a uniform electric field E then t...
Text Solution
|
- If a hemispherical body is placed in a uniform electric field E then t...
Text Solution
|