A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
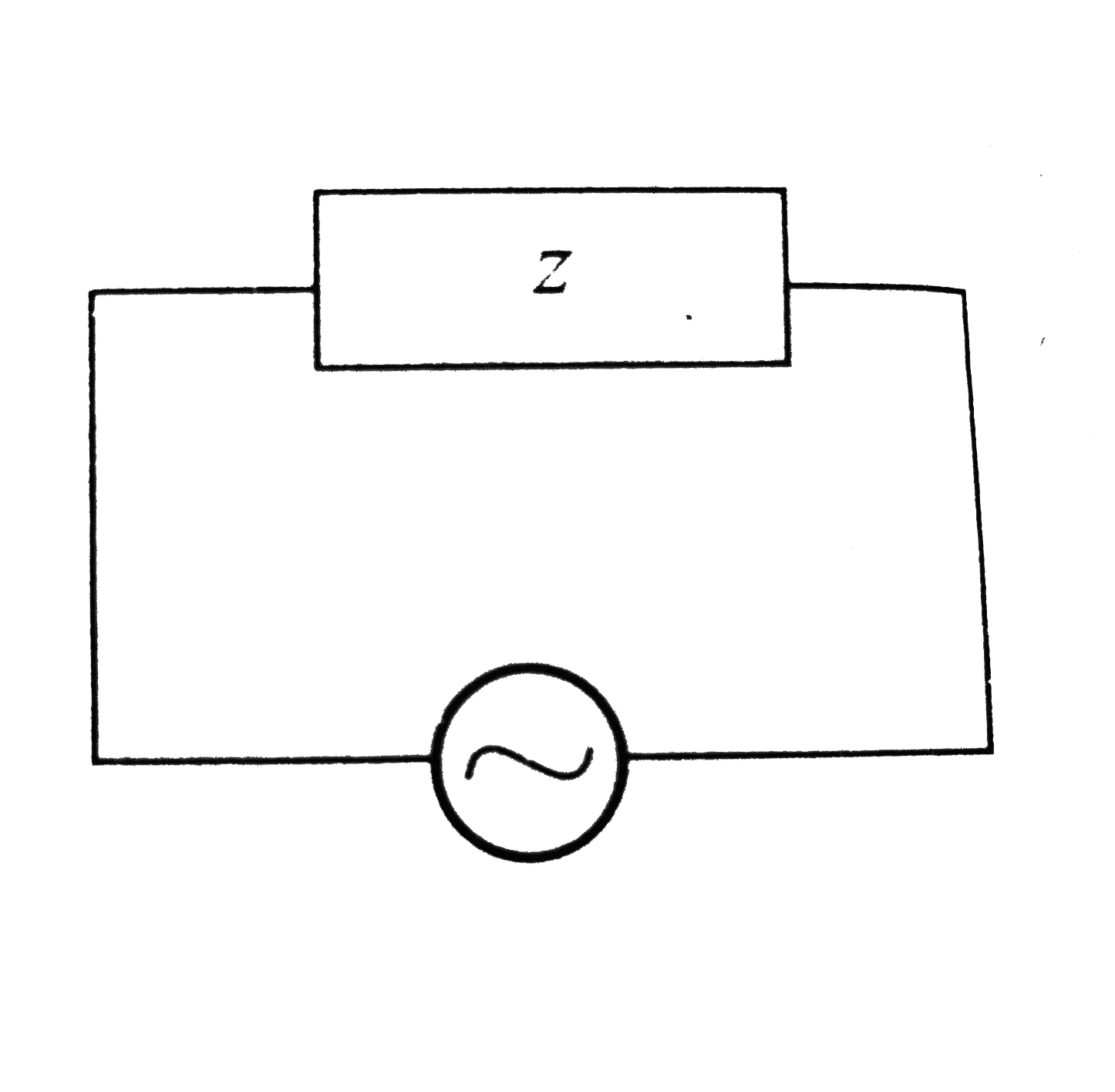
- In a box Z of unknown elements, L or R or any other combintion, an ac ...
Text Solution
|
- In a black box of unknown elements (L or R or any other combination), ...
Text Solution
|
- In any AC circuit the emf (e) and the current (i) at any instant are g...
Text Solution
|
- एक प्रत्यावर्ती धारा परिपथ में किसी क्षण विघुत वाहक बल (E) तथा वैघुत ध...
Text Solution
|
- The alternating emf of e=e(0) sin omegat is applied across capacitor C...
Text Solution
|
- The power dissipated in alternating circuit with voltage e=e(0) sin om...
Text Solution
|
- किसी बिन्दु पर दो तरंगें निम्न समीकरणों द्वारा निरूपित की जाती हैं- E(...
Text Solution
|
- Analternating voltage E= E0 sin omegat is applied to a circuit contain...
Text Solution
|
- Analternating voltage E= E0 sin omegat is applied to a circuit contain...
Text Solution
|