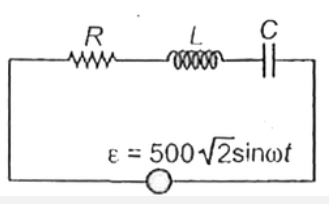
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In a series RLC circuit the r.m.s. voltage across the resistor and the...
Text Solution
|
- In a series LCR circuit, the voltages across an inductor, a capacitor ...
Text Solution
|
- In a series LCR circuit the voltage across an inductor, capacitor and ...
Text Solution
|
- An ac source of 50 V (r.m.s value) is connected across a series R - C ...
Text Solution
|
- In the series L-C-R circuit shown in the figure, the rms voltage acros...
Text Solution
|
- In the given circuit the R.M.S values of voltages across the capacitor...
Text Solution
|
- In a series RLC circuit the r.m.s. voltage across the resistor and the...
Text Solution
|
- In a series LCR circuit the voltage across an inductor, capacitor and ...
Text Solution
|
- In a series LCR circuit, the voltage across an inductor, a capacitor a...
Text Solution
|