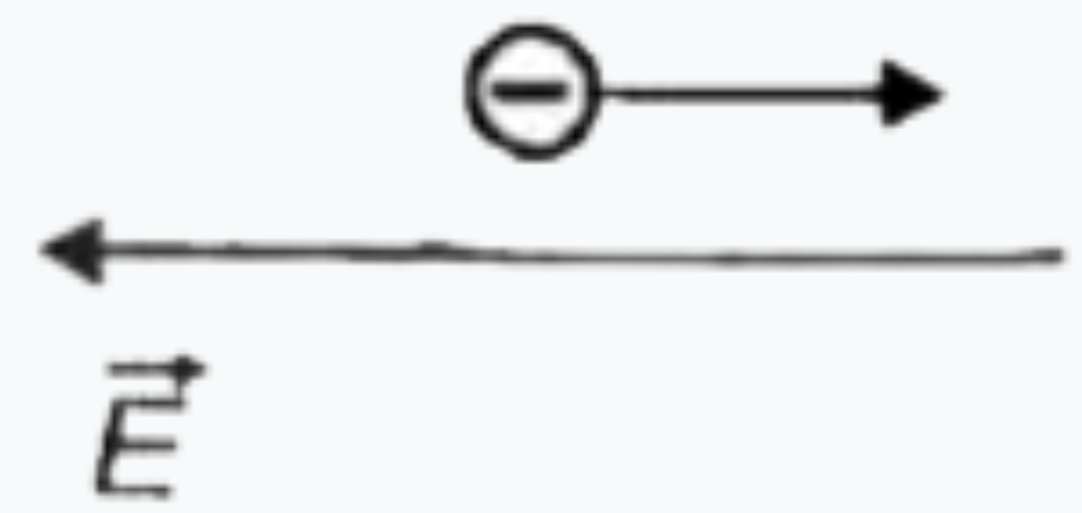
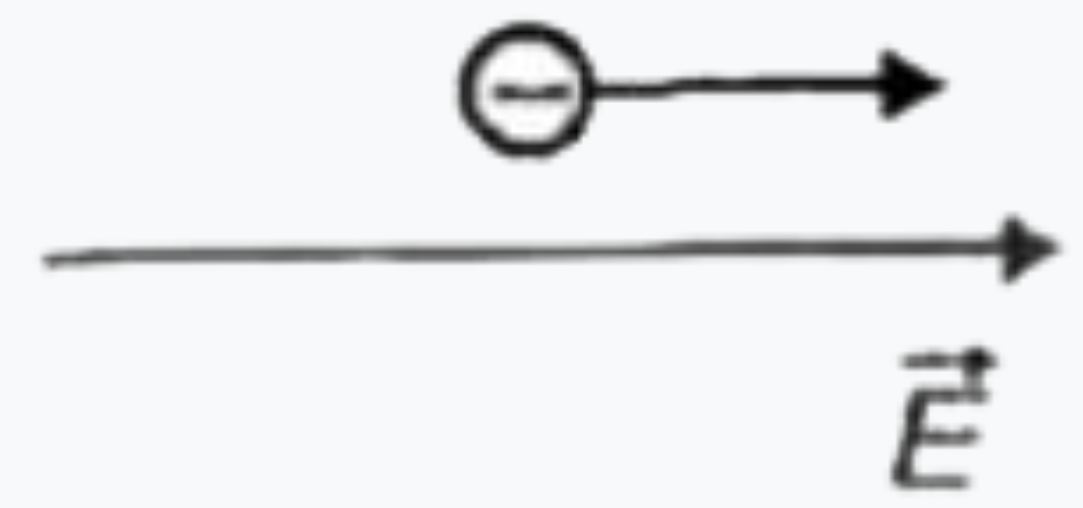
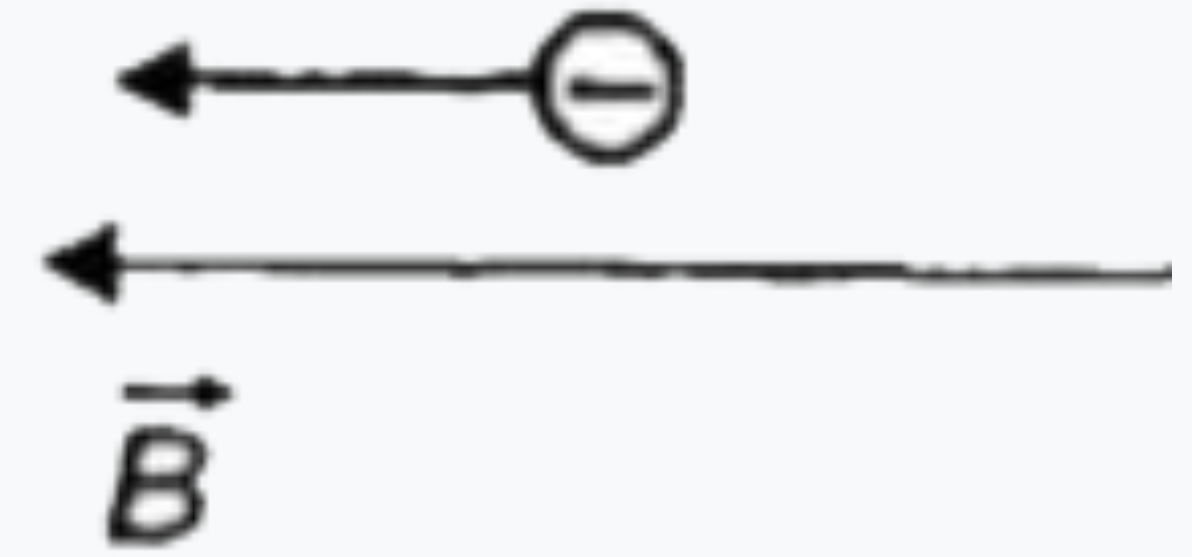
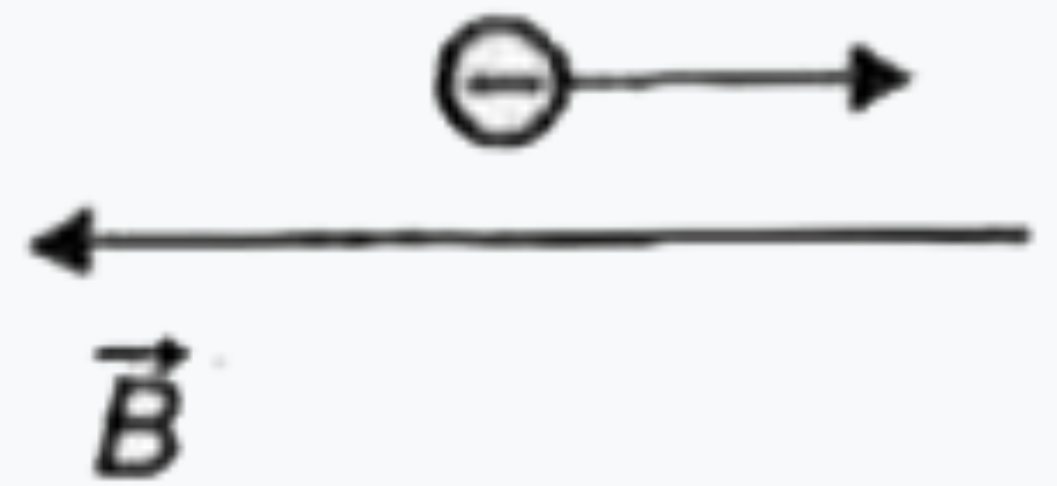
To determine in which case the de Broglie wavelength of an electron is increasing, we can analyze the relationship between the kinetic energy of the electron and its de Broglie wavelength. The de Broglie wavelength (λ) is given by the formula:
\[
\lambda = \frac{h}{\sqrt{2mK.E.}}
\]
where:
- \( h \) is Planck's constant,
- \( m \) is the mass of the electron,
- \( K.E. \) is the kinetic energy of the electron.
From this formula, we can see that the de Broglie wavelength is inversely proportional to the square root of the kinetic energy. This means that if the kinetic energy of the electron decreases, the de Broglie wavelength will increase.
### Step-by-Step Solution:
1. **Identify the Relationship**: Recall that the de Broglie wavelength is inversely proportional to the square root of the kinetic energy of the electron. Thus, if the kinetic energy increases, the wavelength decreases, and if the kinetic energy decreases, the wavelength increases.
2. **Analyze Each Situation**: For each of the four situations provided in the figure, we need to determine whether the kinetic energy of the electron is increasing or decreasing based on the forces acting on it.
3. **Situation 1**: If the force acting on the electron is in the same direction as the electric field, the kinetic energy of the electron will increase. Therefore, the de Broglie wavelength will decrease.
4. **Situation 2**: If the force acting on the electron is opposite to the direction of the electric field, the kinetic energy of the electron will decrease. Therefore, the de Broglie wavelength will increase.
5. **Situation 3**: Analyze the forces and directions similarly. If the force causes the electron to speed up, the kinetic energy increases, and the wavelength decreases. If the force slows it down, the kinetic energy decreases, and the wavelength increases.
6. **Situation 4**: Again, check the direction of the force relative to the electric field. Determine if the kinetic energy is increasing or decreasing.
7. **Conclusion**: After analyzing all four situations, we find that in **Situation 2**, the kinetic energy of the electron decreases, leading to an increase in the de Broglie wavelength.
### Final Answer:
The de Broglie wavelength of the electron is increasing in **Situation 2**.