Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
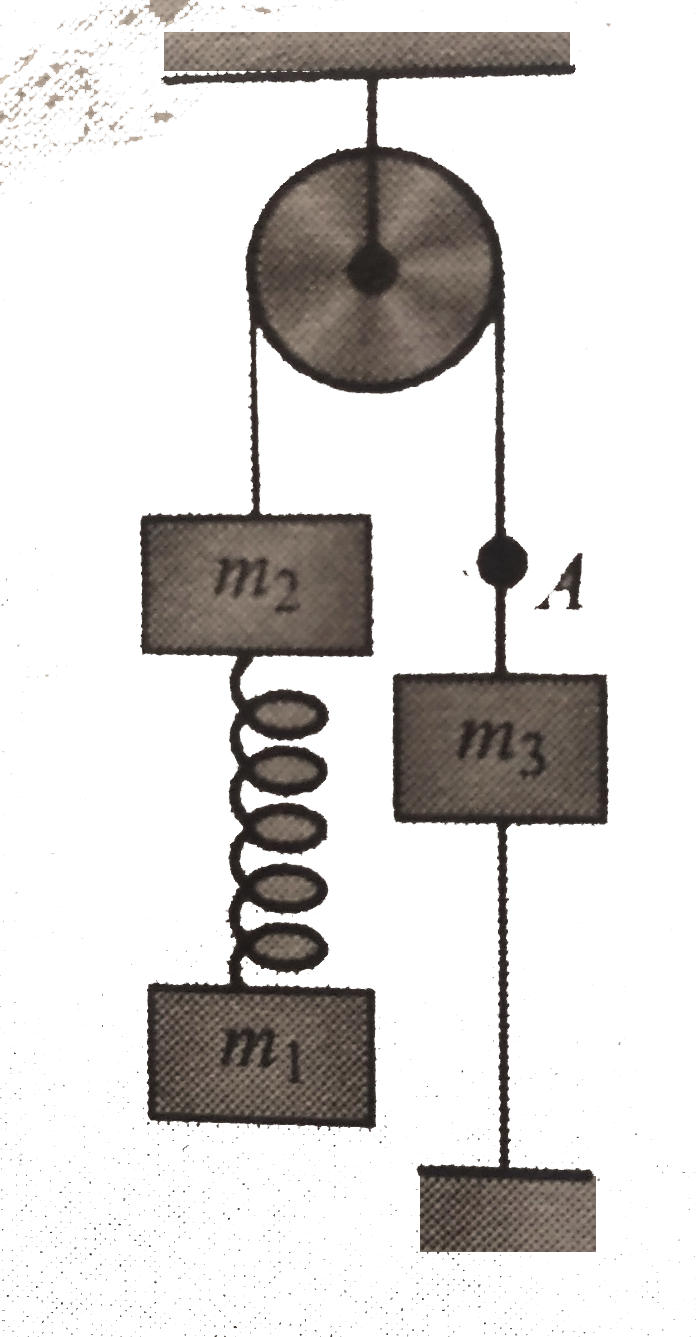
- Three blocks arranged with pullwy and spring as shown in fig. If the s...
Text Solution
|
- Three blocks arranged with pullwy and spring as shown in fig. If the s...
Text Solution
|
- Three blocks m(1), m(2) , and m(3) are arranged as shown in fig. if m(...
Text Solution
|
- Two block of masses m(1) and m(2) are in equilibrium. The block m(2) h...
Text Solution
|
- Figure shows a block of mass m(1) sliding on a block of mass m(2) , wi...
Text Solution
|
- For the system shown in fog. m(1) gt m(2) gtm(3) gt m(4). Initially, t...
Text Solution
|
- Two block of masses m(1) and m(2) are connected as shown in the figure...
Text Solution
|
- Three blocks of masses m(1), m(2) and M are arranged as shown in figur...
Text Solution
|
- (a) shows a block of mass m(1) sliding on a block of mass m(2) , with ...
Text Solution
|