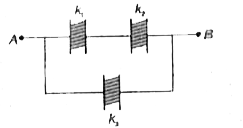
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- If C(AB) (equivalent ) = (C ) /(2) and capacitance of all the capacito...
Text Solution
|
- Find the capacitance between A and B if two dielectric alabs (each of ...
Text Solution
|
- A parallel plate capacitor has capacitance C . If it is equally filled...
Text Solution
|
- In the figure a capacitor is filled with dielectrics K(1), K(2) and K(...
Text Solution
|
- A parallel plate capacitor of area A, plate separation d and capacitan...
Text Solution
|
- The capacitance of a parallel plate capacitor with plate area A and se...
Text Solution
|
- The space between parallel plate capacitors is filled with four dielec...
Text Solution
|
- Two identical parallel plate (air) capacitors c(1) and c(2) have capac...
Text Solution
|
- एक समान्तर प्लेट संधारित्र का क्षेत्रफल A, प्लेटो के मध्य दूरी d और धा...
Text Solution
|