Oblique elastic collision : If the centres of mass of the colliding bodies are not initially moving along the line of impact, then the impact is called oblique collision
Two equal masses undergo oblique elastic will move at right angles after collosion,if the second body initially at rest :
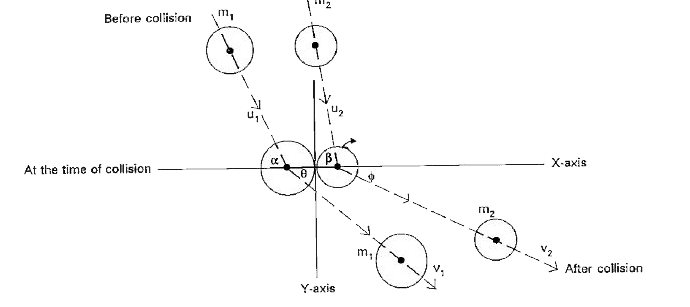
Consider two smooth and perfectly elastic spheres of masses `m_(1) and m_(2) . " Let " u_(1) and u_(2) ` be their initial velocities before collision . Let `v_(1) and v_(2) ` be their final velocities after collision . `(alpha , beta) and (theta, phi) ` are the angles, the directions of motion make with the line of impact before collision and after collision
Since the spheres are smooth, there is no (impulse) change of velocities perpendicular to the time of impact. Hence the resolved part of velocity of the two spheres int he direction perpendicular to the line of impact remain unchanged
`:. v_(1) sin theta = u_(1) sin alpha . . . . (1)`
and `v_(2) sin phi = u_(2) beta . . . (2)`
According to the principle of conservation of momentum, the sum of the moment of the two spheres along the line of impact before collision and after collision are equal .
`:. m_(1) u_(1) cos alpha + m_(2) u_(2) cos beta = m_(1) v_(1) cos theta + m_(2) v_(2) cos phi . . . (3)`
`to m_(1) (u_(1) cos alpha - v_(1) cos theta ) = m_(2) (v_(2) cos phi - u_(2) cos beta) .. . . (4)`
According to the principle of conservation of kinetic energy, the sum of the K.E along the lien of impact before and after are equal
`:. (1)/(2) m_(1) (u_(1) cos alpha) ^(2) + (1)/(2) m_(2) (u_(2) cos beta) ^(2) = (1)/(2) m_(1) (v_(1) cos theta)^(2) + (1)/(2) m_(2) (v_(2) cos phi)^(2)`
`m_(1) [ (u_(1) cos alpha)^(2) - (v_(1) cos theta)^(2) ] = m_(2) [(v_(2) cos phi)^(2) - (u_(2) cos beta)^(2)] . . . (5)`
`((5))/((4)) rArr u_(1) cos alpha + v_(1) cos theta = (v_(2) cos phi + v_(2) cos beta)`
`v_(1) cos theta = v_(2) cos phi + u_(2) cos beta - u_(1) cos alpha . . . . (6)`
and `v_(2) cos phi = v_(1) cos theta + u_(1) cos alpha - u_(2) cos beta . . . . (7)`
sub. equation (6) in equation (3) , we get
`v_(1) cos theta = ((m_(2)- m_(1))/(m_(1) + m_(2))) u_(1) cos alpha + 2 ((m_(2) u_(2))/(m_(1) + m_(2))) cos beta . . . . (8)`
and ` v_(2) cos phi = ((m_(2) - m_(1))/(m_(1) + m_(2))) u_(2) cos beta + ((2m_(1) u_(1))/(m_(1) = m_(2))) cos alpha . . . (9)`
If `u_(2) = 0 and m_(1) = m_(2)` then equation (2) we get `phi = 0 ` and from equation `(8) , theta = 90^(@)` . This means that if a sphere of mass .m. collides obliquely on another perfectly elastic sphere of the same mass at rest the directions of motions of the spheres after impact will be at right angles
