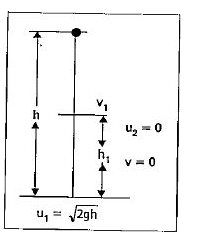
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Derive an expression for the height attained by a freely falling body ...
Text Solution
|
- A body falling from a height of 10 m rebounds from the hard floor . It
Text Solution
|
- A body falling from a height of 10m rebounds from hard floor. If it lo...
Text Solution
|
- A body freely falling from a certain height 'h' , after striking a smo...
Text Solution
|
- Derive an expression for the height attained by a freely falling body ...
Text Solution
|
- A ball of mass M falls from a height on a floor for which the coeffici...
Text Solution
|
- In the case of a body freely falling from small height
Text Solution
|
- A body falls on the ground from a height of 10 metre and rebounds to a...
Text Solution
|
- In the case of a body freely falling from small height
Text Solution
|