Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
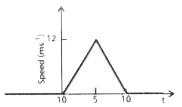
- The speed-time graph of a particle moving along a fixed direction is s...
Text Solution
|
- The speed-time graph of a particle moving along a fixed direction is s...
Text Solution
|
- The speed-time graph of a particle moving along a fixed direction as s...
Text Solution
|
- किसी निश्चित दिशा के अनुदिश चल रहे किसी कण का चाल-समय ग्राफ चित्र 3.28...
Text Solution
|
- किसी निश्चित दिशा में अनुदिश चल रहे किसी कण का चाल-समय ग्राफ चित्र मे...
Text Solution
|
- किसी निश्चित दिशा में अनुदिश चल रहे किसी कण का चाल - समय ग्राफ चित्र 3...
Text Solution
|
- The speed time graph of a particle moving along a fixed direction is a...
Text Solution
|
- The speed - time graph of a particle moving along a solid curve is sho...
Text Solution
|
- The speed-time graph of a particle moving along a fixed direction is s...
Text Solution
|