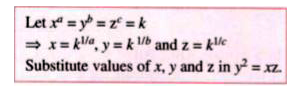Topper's Solved these Questions
CHAPTERWISE REVISION (STAGE 1)
ICSE|Exercise logrithms|20 VideosCHAPTERWISE REVISION (STAGE 1)
ICSE|Exercise Triangles|18 VideosCHAPTERWISE REVISION (STAGE 1)
ICSE|Exercise Simultaneous Equations|18 VideosCHAPTER REVISION (STAGE 2)
ICSE|Exercise DISTANCE FORMULA |12 VideosCHAPTERWISE REVISION (STAGE 3)
ICSE|Exercise DISTANCE FORMULA |11 Videos
Similar Questions
Explore conceptually related problems
ICSE-CHAPTERWISE REVISION (STAGE 1) -Indices
- If 25 ^(x+1) = (125)/( 5^(x)) , find the value of x.
Text Solution
|
- If 8^(x) xx 4^(y) = 32 and 81 ^(x) xx 27 ^(y) = 3 , find the valu...
Text Solution
|
- Given ((8)/(27))^(x- 1) = ((9)/(4))^(2x+ 1) , find the value of x .
Text Solution
|
- Evaluate: sqrt(( 1)/(4)) + (0.01) ^(-(1)/(2)) xx (5) - (27)^((2...
Text Solution
|
- Evaluate : ((1)/(4)) ^(-2) - 3 (32)^((2)/(5)) xx ( 7) ^(0) +((9...
Text Solution
|
- If x^(a) = y^(b) = z^ (c ) and y^(2) = xz, prove that b= ( 2ac)...
Text Solution
|
- Evaluate : (1)/( ( 216)^((-2)/(3)) ) + (1)/((27) ^((-4)/(3)))
Text Solution
|
- Evaluate : [5(8^((1)/(3))+ 27 ^((1)/(3))) ^(3) ]^((1)/(4))
Text Solution
|
- If ((3(1)/(4) )^(4) -(4( 1)/(3))^(4))/( (3,(1)/(4) )^(2) -(4,(1)/(3))...
Text Solution
|
- Solve for x and y , if : (sqrt( 27) )^(x) ÷ 3^(y+ 4) = 1 and 8^(...
Text Solution
|
- If a= -1 and b= 2 find : a^(2) + b^(2)
Text Solution
|
- If a= -1 and b= 2 find : a^(b) - b^(a)
Text Solution
|
- If a= -1 and b= 2 find : a^(b) xx b^(a)
Text Solution
|
- If a= -1 and b= 2 find : a^(b) // b^(a)
Text Solution
|