Topper's Solved these Questions
CHAPTER REVISION (STAGE 2)
ICSE|Exercise CONSTRUCTIONS OF POLYGONS |19 VideosCHAPTER REVISION (STAGE 2)
ICSE|Exercise STATISTICS |2 VideosCHAPTER REVISION (STAGE 2)
ICSE|Exercise MID-POINT THEOREM |12 VideosAREA THEOREMS
ICSE|Exercise Exercies 16(C )|22 VideosCHAPTERWISE REVISION (STAGE 1)
ICSE|Exercise Graphical solution |10 Videos
Similar Questions
Explore conceptually related problems
ICSE-CHAPTER REVISION (STAGE 2) -RECTILINEAR FIGURES
- In the given figures ABCD is a trapezium with DC //AB , angle AOB = ...
Text Solution
|
- The perimeter of a parallelogram ABCD = 40 cm , AB = 3x cm, BC = 2...
Text Solution
|
- ABCDE is a pentagon in which AB = AE, BC = ED and angle ABC = ang...
Text Solution
|
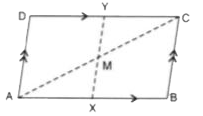
- In the parallelogram ABCD ,M is mid-point of AC and X,Y are poin...
Text Solution
|