Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ICSE-EQUATION OF A LINE-EXERCISE 14(E)
- Point A and B have co-ordinates (7, -3) and (1,9) respectively. Find :...
Text Solution
|
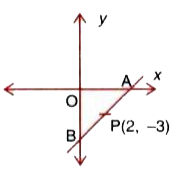
- A and B are two points on the x-axis and y-axis respectively. P(2, -3)...
Text Solution
|
- A and B are two points on the x-axis and y-axis respectively. P(2, -3)...
Text Solution
|
- A and B are two points on the x-axis and y-axis respectively. P(2, -3)...
Text Solution
|
- The equation of a line is 3x + 4y - 7 = 0. Find: the slope of the li...
Text Solution
|
- The equation of a line is 3x + 4y - 7 = 0. Find: the equation of a l...
Text Solution
|
- ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, -4). ...
Text Solution
|
- ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D 2, -4...
Text Solution
|
- Given equation of line L1 is y = 4 Write the slope of line L1 if...
Text Solution
|
- Given equation of line L1 is y = 4 Write the co-ordinates of po...
Text Solution
|
- Given equation of line L1 is y = 4 Find the equation of L2.
Text Solution
|
- Find : equation of AB
Text Solution
|
- Find : equation of CD
Text Solution
|
- Find the equation of the line that has x-intercept = -3 and is perpend...
Text Solution
|
- A straight line passes through the points P(-1, 4) and Q(5,-2). It int...
Text Solution
|
- A straight line passes through the points P(-1, 4) and Q(5,-2). It int...
Text Solution
|
- A straight line passes through the points P(-1, 4) and Q(5,-2). It int...
Text Solution
|
- In the given figure, line AB meets y-axis at point A. Line through C(2...
Text Solution
|
- In the given figure, line AB meets y-axis at point A. Line through C(2...
Text Solution
|
- In the given figure, line AB meets y-axis at point A. Line through C(2...
Text Solution
|