Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CHAPTERWISE REVISION EXERCISE
ICSE|Exercise CHAPTERWISE REVISION EXERCISE (TANGENTS AND INTERSECTING CHORDS)|10 VideosCHAPTERWISE REVISION EXERCISE
ICSE|Exercise CHAPTERWISE REVISION EXERCISE (CONSTRUCTION)|3 VideosCHAPTERWISE REVISION EXERCISE
ICSE|Exercise CHAPTERWISE REVISION EXERCISE (LOCI)|7 VideosBANKING (RECURRING DEPOSIT ACCOUNTS)
ICSE|Exercise QUESTIONS|7 VideosCIRCLES
ICSE|Exercise EXERCISE 17( C ) |28 Videos
Similar Questions
Explore conceptually related problems
ICSE-CHAPTERWISE REVISION EXERCISE-CHAPTERWISE REVISION EXERCISE (CIRCLES)
- In the given figure, angleADC= 130^(@) and BC= BE. Find angleCBE if AB...
Text Solution
|
- In the given figure, angleOAB= 30^(@) and angleOCB= 57^(@), find angle...
Text Solution
|
- In the given figure, O is the centre of the circle. If chord AB= chord...
Text Solution
|
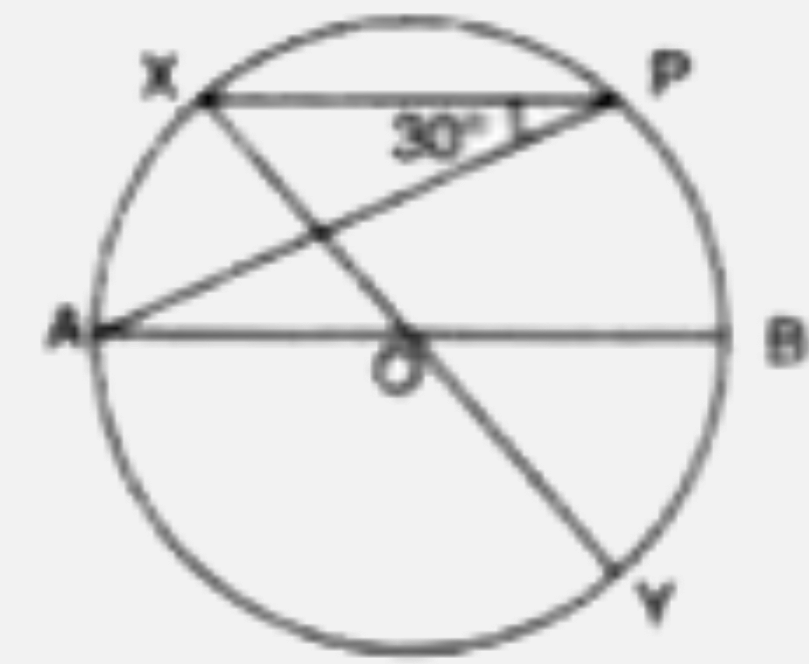
- In the given figure, AB and XY are diameters of a circle with centre O...
Text Solution
|
- In the given figure, AB and XY are diameters of a circle with centre O...
Text Solution
|
- In the given figure, AB and XY are diameters of a circle with centre O...
Text Solution
|
- In the given figure, AB and XY are diameters of a circle with centre O...
Text Solution
|
- In the adjoining figure, AB= AD, BD= CD and angleDBC= 2 angleABD Pro...
Text Solution
|
- AB is a diameter of a circle with centre O. Chord CD is equal to radiu...
Text Solution
|