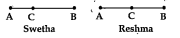Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT TELUGU-MEASURES OF LINES AND ANGLES-EXERCISE - 5.3
- Mid point of overline(AB) is located by Swetha and Reshma like this. W...
Text Solution
|
- Which of the following are models for parallel lines, perpendicular li...
Text Solution
|
- Which of the following are models for parallel lines, perpendicular li...
Text Solution
|
- Which of the following are models for parallel lines, perpendicular li...
Text Solution
|
- Which of the following are models for parallel lines, perpendicular li...
Text Solution
|
- Which of the following are models for parallel lines, perpendicular li...
Text Solution
|
- Trace the copy of set squares(Geometry box) on a paper and mark the pe...
Text Solution
|
- ABCD is a rectangle.BarAC and bar BD.Write the pairs of parallel lines...
Text Solution
|
- ABCD is a rectangle.BarAC and bar BD.Write the pairs of parallel lines...
Text Solution
|
- ABCD is a rectangle. bar(AC) and bar(BD) are diagonals. Write the pai...
Text Solution
|