Similar Questions
Explore conceptually related problems
Recommended Questions
- Blockes A and B are resting on a smooth horizontal surface given equal...
Text Solution
|
- A spring block system is kept inside the smooth surface of a trolley a...
Text Solution
|
- A long block A is at rest on a smooth horizontal surface. A small bloc...
Text Solution
|
- Two blocks of masses m and 2m are placed on a smooth horizontal surfac...
Text Solution
|
- A block is kept on a rough horizontal surface. A variable horizontal f...
Text Solution
|
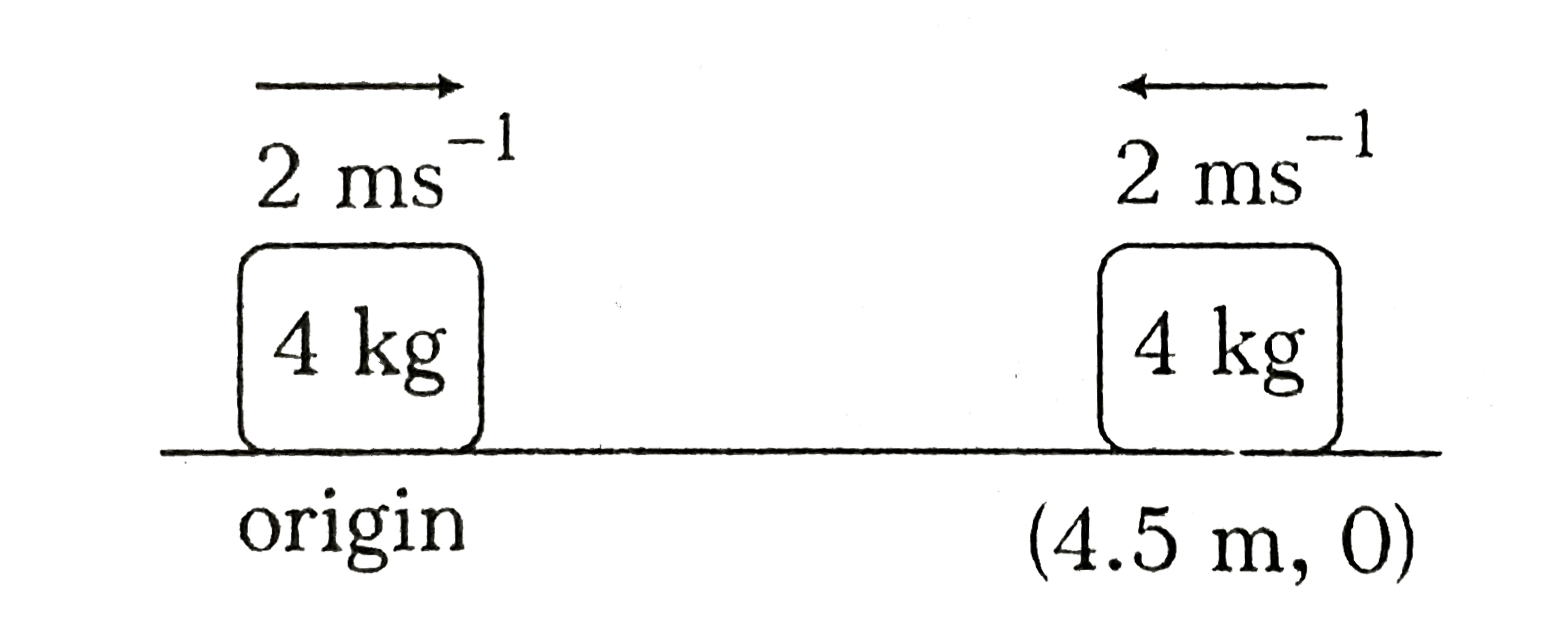
- Blocks are given velocities as shown at t=0, find velocity and positio...
Text Solution
|
- In the spring-block system shown, the block oscillates on a smooth hor...
Text Solution
|
- Blocks A and B are resting on a smooth horizontal surface given equal ...
Text Solution
|
- A force of 50N acts in the direction as shown in figure. The block of ...
Text Solution
|