Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-REVISION DPP-All Questions
- A solid sphere (radius = R) rolls without slipping in a cylindrical th...
Text Solution
|
- Two opposite forcesF(1) = 120 N and F(2) = 80 N act on an elastic plan...
Text Solution
|
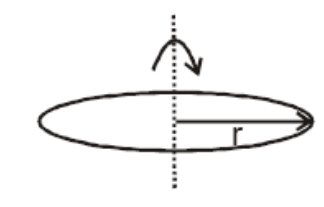
- A ring of radius r made of wire of density rho is rotated about a stat...
Text Solution
|
- The length of an elastic string is 5 metre when the longitudinal tensi...
Text Solution
|
- A block of mass m=2kg of shown dimensions is placed on a plank of mass...
Text Solution
|
- There are two ideal springs of force constants K1 and K2 respectively....
Text Solution
|
- There are two ideal springs of force constants K1 and K2 respectively....
Text Solution
|
- There are two ideal springs of force constants K1 and K2 respectively....
Text Solution
|
- A rod of mass 'm and length L is attached to a L shaped plank at 'A'. ...
Text Solution
|
- A rod of mass 'm and length L is attached to a L shaped plank at 'A'. ...
Text Solution
|
- A rod of mass 'm and length L is attached to a L shaped plank at 'A'. ...
Text Solution
|
- Two blocks A and B of masses m and 2m are placed on a smooth horizonta...
Text Solution
|
- A uniform rod of mass M and length L, area of cross section A is place...
Text Solution
|
- A uniform rod of mass M and length L, area of cross section A is place...
Text Solution
|
- In Young's double slit experiment, the distance between two slits is m...
Text Solution
|
- A particle of mass m = 1 kg excutes SHM about mean position O with ang...
Text Solution
|
- In a spring block system on a horizontal smooth surface. K = spring co...
Text Solution
|
- A container open from top, filled with water (density rhow) upto the t...
Text Solution
|
- A uniform solid sphere of radius R is in equilibrium inside a liquid w...
Text Solution
|
- A large open tank is filled with water upto a height H. A small hole i...
Text Solution
|