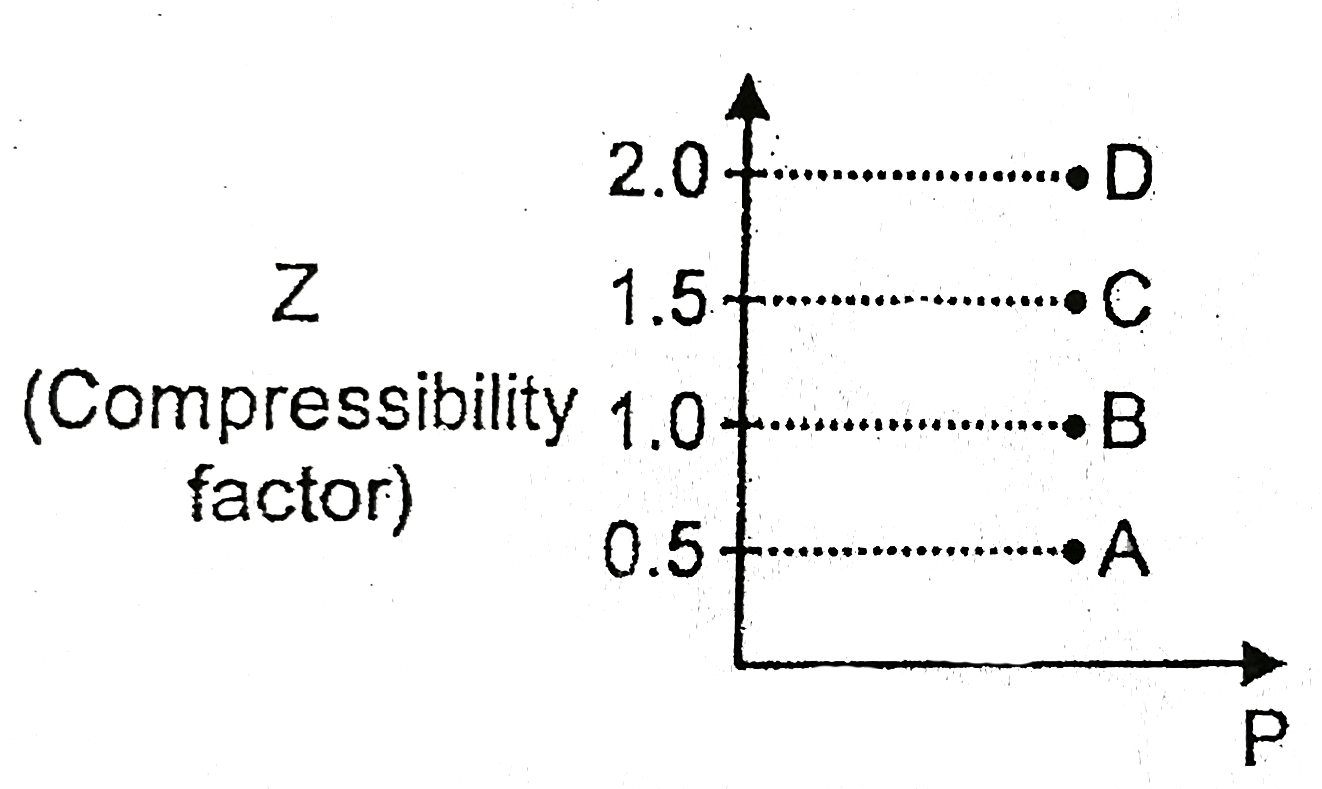A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Molar volume of an Ideal gas is 0.45 dm^(3)//mol. The molar volume of ...
Text Solution
|
- 1 mol e of an ideal monoatomic gas is mixed with 1 mol e of an ideal d...
Text Solution
|
- If bar(V) is the observed molor volume of real gas and bar(V)(id) is t...
Text Solution
|
- Molar volume of an Ideal gas is 0.45 dm^(3)//mol . The molar volume of...
Text Solution
|
- For a real gas, if at critical conditions molar volume of gas is 8.21 ...
Text Solution
|
- What is molar volume of an ideal gas under N.T.P. conditions ?
Text Solution
|
- 5 mol of an ideal gas expand reversibly from a volume of 8 dm^(3) to 8...
Text Solution
|
- 3.32 bar पर 5 dm^(3) आयतन घेरने वाली 4.0 mol गैस के ताप की गणना कीजिए ...
Text Solution
|
- The ratio of the molar volume of the real gas to the molar volume of t...
Text Solution
|