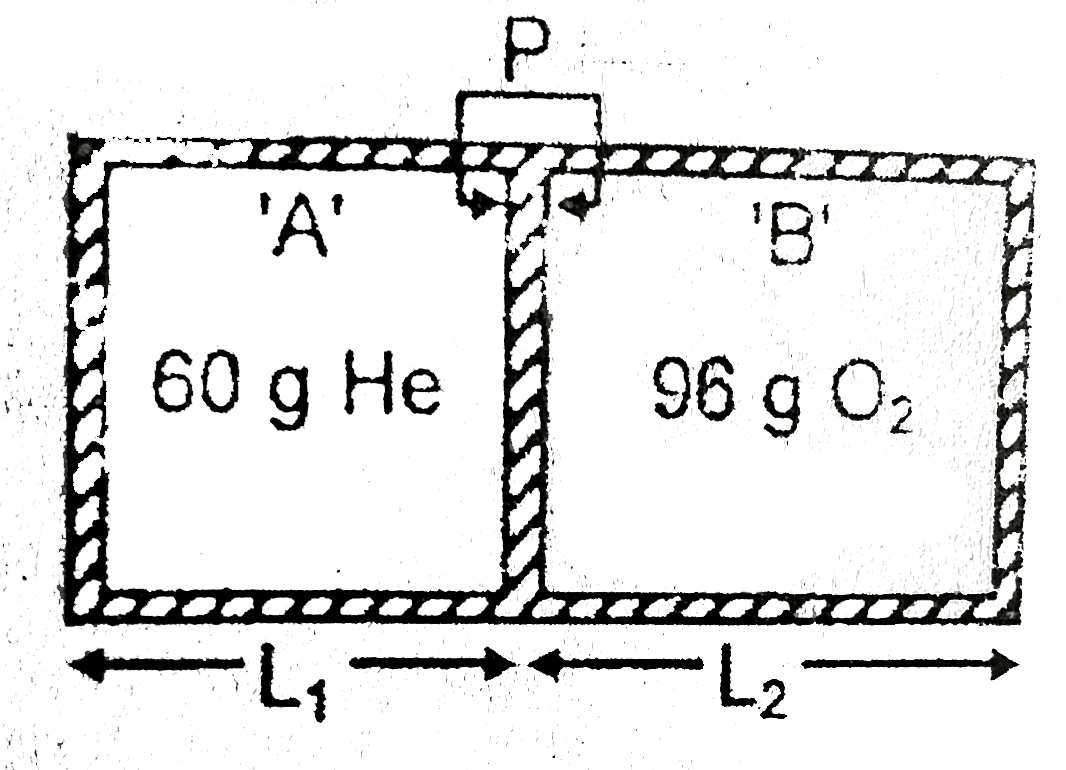A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A cylindrical diathemic chamber fitted with movable, massless & fricti...
Text Solution
|
- A cylindrical diathemic chamber fitted with movable, massless & fricti...
Text Solution
|
- Comprehension-2 A mono atomic ideal gas is filled in a non conducting...
Text Solution
|
- A gas fills the right portion of a horizontal cylinder whose radius is...
Text Solution
|
- A diathermic piston divides adiabatic cylinder of volume V0 into two e...
Text Solution
|
- A gas filled in a cylinder fitted with movable piston is allowed to ex...
Text Solution
|
- A gas is filled in a cylinder fitted with a piston at a definite tempe...
Text Solution
|
- एक घर्षणहीन पिस्टन सिलिण्डर में एकपरमाणुक गैस ताप T(1) पर भरी है | पि...
Text Solution
|
- गैस से भरे हुए एक बन्द ऊर्ध्वाधर बेलनाकार बर्तन को एक घर्षणहीन एवं नगण...
Text Solution
|