Home
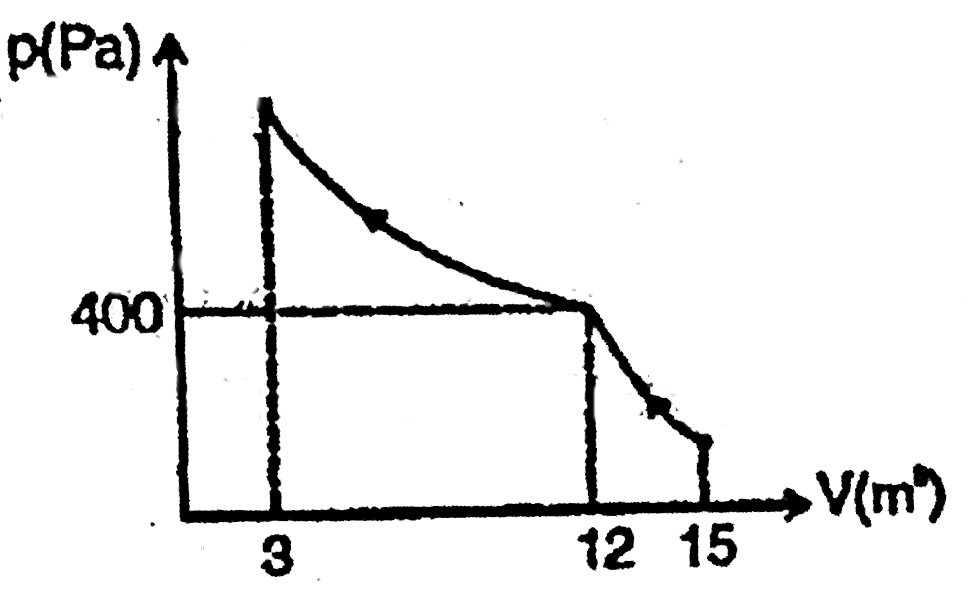
Class 11
PHYSICS
Curve in the figure shows an adiabatic c...

Curve in the figure shows an adiabatic compression of an ideal gas from `15m^3` to `12m^3`, followed by an isothermal compression to a final volume of `3.0m^3`. There are 2.0 moles of the gas. Total heat supplied to the gas is equal to: (ln2= 0.693)

A

`4521 J`

B

`-4521 J`

C

`-6653 J`

D

`-8476 J`

Text Solution

Verified by Experts

The correct Answer is:
C
There is no heat transfer in adiabatic compression. In isothermal process
`Q = W = P_(1) V_(1) In(V_(2))/(V_(1)) = 400 xx 12 In (1)/(4) =- 653 J`
Promotional Banner

Topper's Solved these Questions

  • KTG & THERMODYNAMICS

    RESONANCE ENGLISH|Exercise PART -III|25 Videos

  • KTG & THERMODYNAMICS

    RESONANCE ENGLISH|Exercise PART -IV|9 Videos

  • KTG & THERMODYNAMICS

    RESONANCE ENGLISH|Exercise Exercise-2|1 Videos

  • KINETIC THEORY OF GASES AND THERMODYNAMICS

    RESONANCE ENGLISH|Exercise Exercise|64 Videos

  • MAGNETIC FIELD AND FORCES

    RESONANCE ENGLISH|Exercise Exercise|64 Videos

Similar Questions

Explore conceptually related problems

An ideal gas occupies a volume of 2m^(3) at a pressure of 3xx10^(6) p,a the energy of the gas is :

An ideal monoatomic gas occupies volume 10^(-3)m^(3) at temperature 3K and pressure 10^(3) Pa. The internal energy of the gas is taken to be zero at this point. It undergoes the following cycle: The temperature is raised to 300K at constant volume, the gas is then expanded adiabatically till the temperature is 3K , followed by isothermal compression to the original volume . Plot the process on a PV diagram. Calculate (i) The work done and the heat transferred in each process and the internal energy at the end of each process, (ii) The thermal efficiency of the cycle.

A cylinder contains 0.50 mol of an ideal gas at temperature of 310 K. as the gas expands isothermally from an initial volume of 0.31 m^(3) to a final volume of 0.45 m^(3) , find the amount of heat that must be added to the gas in order to maintain a constant temperature.

Calculate the change in molar Gibbs energy of carbon dioxide gas at 20^(@) C when it is isothermally compressed from 1.0 bar to 2.0 bar.

The pressure of a gas is 100 k Pa. if it is compressed from 1 m^(3) to 10 dm^(3) , find the work done .

One mole of an ideal gas (C_(v,m)=(5)/(2)R) at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas is :

A diatomic ideal gas undergoes a thermodynamic change according to the P-V diagram shown in the figure. The total heat given to the gas is nearly ( use ln2=0.7):

A diatomic ideal gas undergoes a thermodynamic change according to the P-V diagram shown in the figure. The total heat given to the gas is nearly ( use ln2=0.7):

An ideal gas (gamma = (5)/(3)) is adiabatically compressed from 640 cm^(3) to 80cm^(3) . If the initial pressure is P then find the final pressure?

One mole of ideal gas (C_(P, m) = 15 JK^(-1) "mole"^(-1)) follow the process as shown in figure.