Home
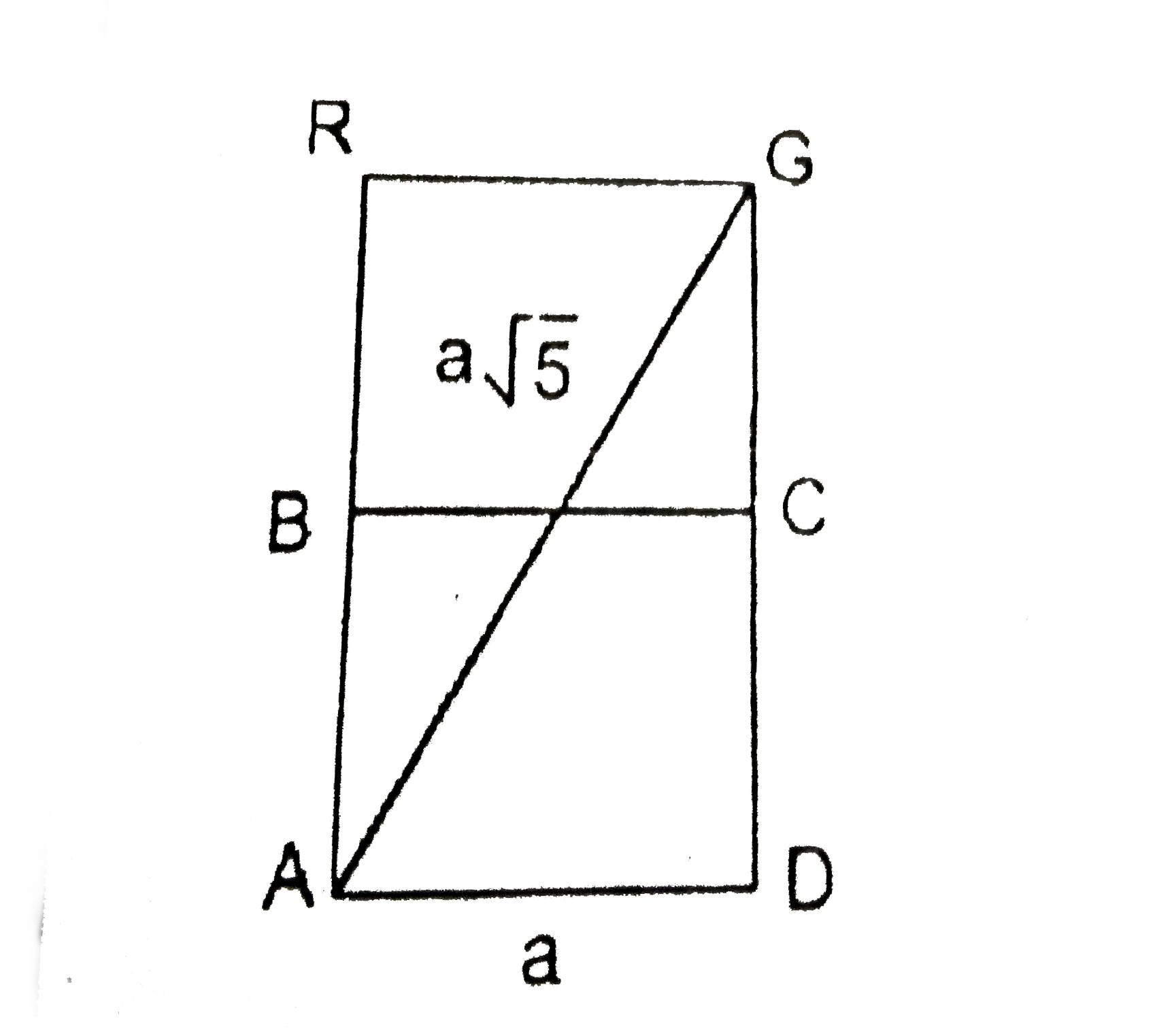
Class 11
PHYSICS
An ant is at a corner of a cubical room ...

An ant is at a corner of a cubical room of side a. The ant can move with a constant speed u. The minimum time taken to reach the farthest corner of the cube is

A

`(3a)/(u)`

B

`(sqrt(3a))/(u)`

C

`(sqrt(5a))/(u)`

D

`((sqrt(2)+1)a)/(u)`

Text Solution

Verified by Experts

The correct Answer is:
C
` (##RES_PHY_DPP_12_XI_E01_111_S01.png" width="80%">
on placing back face and bottom face in same plane.

`A rarr` starting point `G rarr ` final point
minimum time `=(sqrt(5)a)/(u)`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise Dpp no. 13 physics|5 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise DPP NO. 14 PHYSICS|10 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise Compreshension|6 Videos

  • CURRENT ELECTRICITY

    RESONANCE ENGLISH|Exercise Exercise|53 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

Six particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.

Figure shows an imaginary cube of side a. A uniformly charged rod of length a moves towards right at a constant speed v. At t=0 the right end of the just touches the left face of the cube. Plot a graph between electric flux passing through the cube versus time.

Four persons A, B, C and D initially at the corners of a square of side of length d. If every person starts moving with same speed v such that each one faces the other always, the person will meet after time

In the figure the top view of a compartment of a train is shown. A man is sitting at a corner 'B' of the compartment . The man throws a ball ( with respect to himself ) along the surface of the floor towards the corner 'D' of the compartment of the train. The ball hits the corner 'A' of the compartment, then find the time at which it hits A after the ball is thrown . Assume no other collision during motion and floor is smooth. The length of the compartment is given 'l' and the train is moving with constant acceleration 'a' in the direction shown in the figure.

Two men P & Q are standing at corners A & B of square ABCD of side 8m. They start moving along the track with constant speed 2 m//s and 10 m//s respectively. Find the time when they will meet for the first time

Four particles A, B, C and D are situated at the corner of a square ABCD of side a at t-0. Each of particles moves with constant speed (v). A always has its velocity along AB, B along BC, C along CD~ and D along DA . At what time will these particles meet each other ?

A body is projected up with a speed u and the time taken by it is T to reach the maximum height H. Pich out the correct statement

From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is

From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is

Two men P & Q are standing at corners A & B of square ABCD of side 8m. They start moving along the track with constant speed 2(m)/(s) and 10(m)/(s) respectively. Find the time when they will meet for the first time