Home
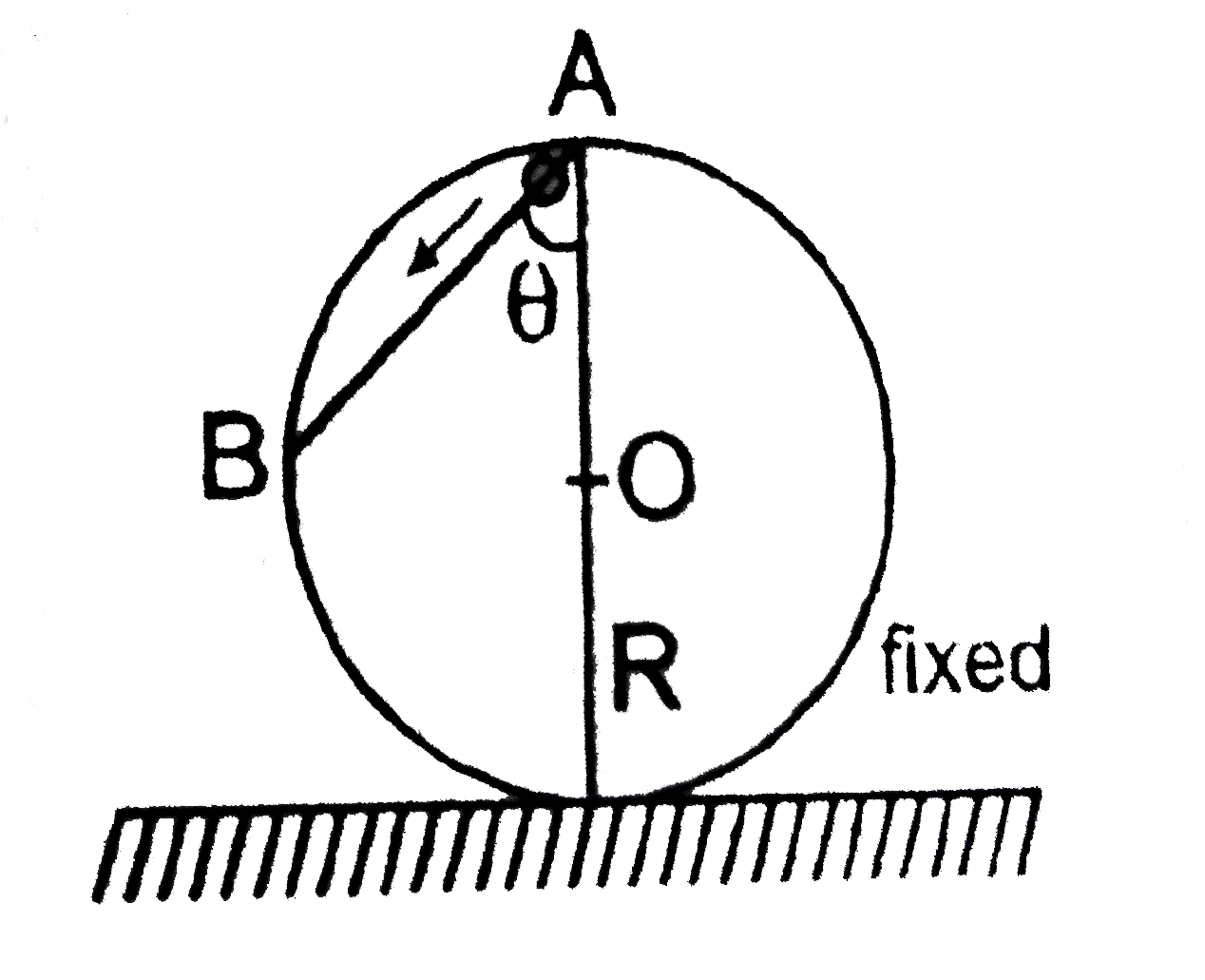
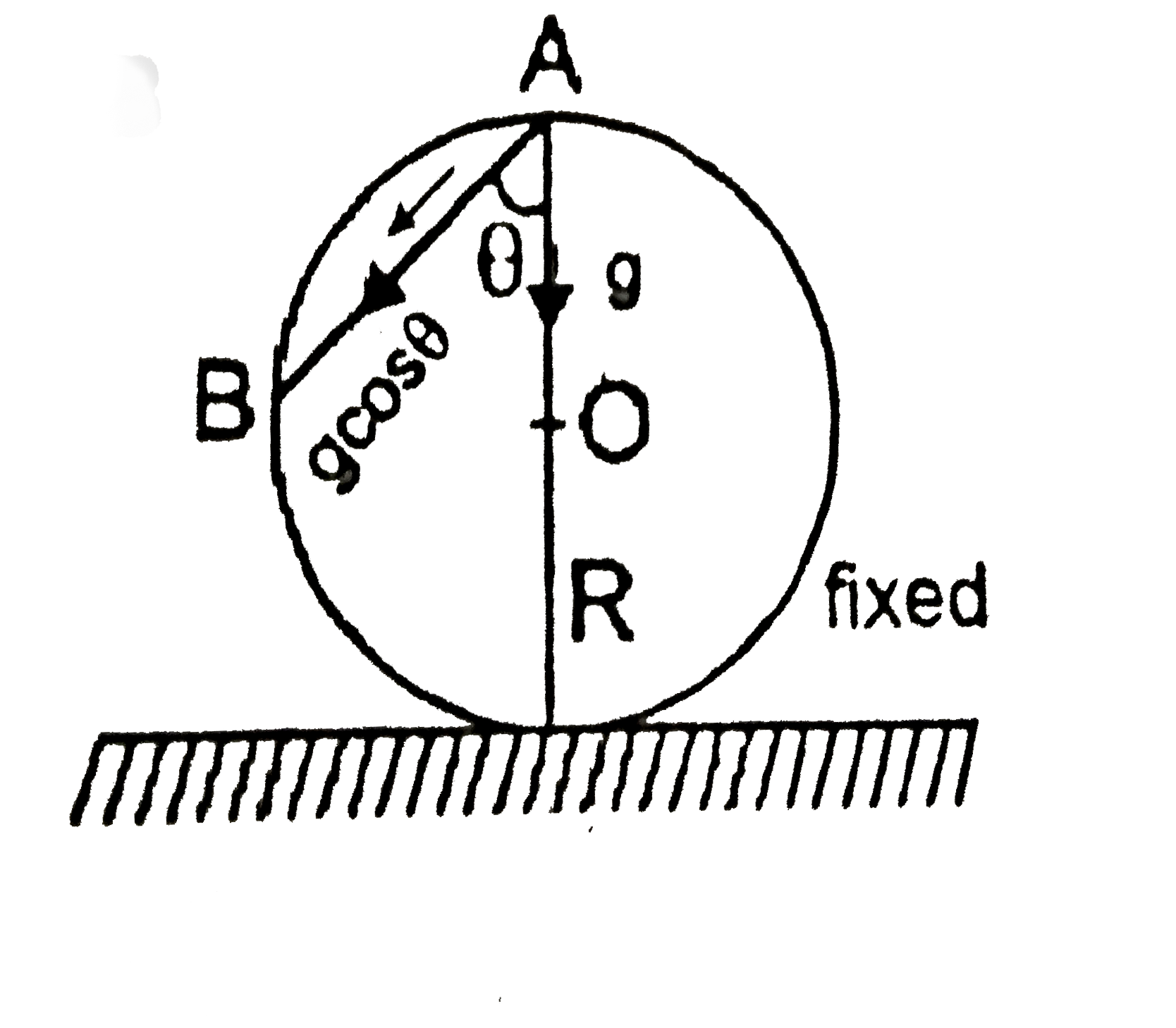
Class 11
PHYSICS
A frictionless wire is fixed between A ...

A frictionless wire is fixed between `A` and `B` inside of a hollow sphere of radius `R` as shown. A beam slips along the wire starting from the rest at point `A`. The time taken by the beam to slip from `A` to `B` will be

A

`2sqrt(R//g)`

B

`gRsqrt(gcostheta)`

C

`(2sqrt(gR))/(gcostheta)`

D

`(2sqrt(gRcostheta))/(g)`

Text Solution

Verified by Experts

The correct Answer is:
A
`AB=2R cos theta`
acceleration along `AB`
`a=g cos theta`
`u=0` from `A` to `B`
`S=ut+(1)/(2)at^(2)`

`2R cos theta=0+(1)/(2)(g cos theta)t^(2)`
`t=2sqrt((R)/(g))`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 22.|8 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp23|8 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 20|8 Videos

  • CURRENT ELECTRICITY

    RESONANCE ENGLISH|Exercise Exercise|53 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

A frictionless wire is fixed between A and B inside a circle of radius R . A small bead slips along the wire. Find the time taken by the bead to slip from A to B .

A bead is free to slide down on a smooth wire rightly stretched between points A and B on a vertical circle of radius 10 m . Find the time taken by the bead to reach point B , if the bead slides from rest from the highest point A on the circle. .

A wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is

A point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R//2 from the centre of the sphere is

A bead is free to slide down a smooth wire tightly stretched between points A and on a verticle circle of radius R. if the bead starts from rest at 'A', the highest point on the circle, its velocity when it arrives at B is :-

A hollow sphere of radius r is put inside another hollow sphere of radius R. The charges on the two are +Q and -q as shown in the figure. A point P is located at a distance x from the common centre such that r lt x lt R . The potential at the point P is

A spherical conductor A of radius r is placed concentrically inside a conducting shell B of radius R(R gt r) . A charge Q is given to A , and then A is joined to B by a metal wire. The charge flowing from A to B will be

The disc of radius r is confined to roll without slipping at A and B . If the plates have the velocities shown, then

A particle of mass m is projected with speed sqrt(Rg/4) from top of a smooth hemisphere as shown in figure. If the particle starts slipping from the highest point, then the horizontal distance between the point where it leaves contact with sphere and the point at which the body was placed is

A sphere and circular disc of same mass and radius are allowed to roll down an inclined plane from the same height without slipping. Find the ratio of times taken by these two to come to the bottom of incline :