Home
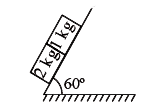
Class 11
PHYSICS
In the figure shown, if friction coeffic...

In the figure shown, if friction coefficient of block 1 kg and 2kg with inclined plane is `mu_(1) = 0.5` and `mu_(2) = 0.4` respectively, then

A

both block will move together

B

both block will move separately

C

there is non`-` zero contact force between two blocks

D

None of these

Text Solution

Verified by Experts

The correct Answer is:
B
If we consider block `2 &1` independently then there accelerations would be for block `(1)`
`a_(1)=g sin theta -mu_(1)g cos theta = g [(sqrt(3))/(2)-(1)/(2)xx(1)/(2)]`
`=(g[2sqrt(3)-1])/(4)`
for block `(2)`
`a_(2)=g sin theta -mu_(2)g cos theta =g[(sqrt(3))/(2)-(2)/(5)xx(1)/(2)]`
`=(g)/(10)[5sqrt(3)-2]`
since `a_(2)gta_(1)` so both block will move separately.
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 33|8 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 34|5 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 31|7 Videos

  • CURRENT ELECTRICITY

    RESONANCE ENGLISH|Exercise Exercise|53 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

In the figure shown if friction co-efficient of block 1 and 2 with inclined plane is mu_1=0.5 and mu_2=0.4 respectively, then find out the correct statement.

Two blocks of masses m_1 = 4 kg and m_2 = 2kg connected by a massless rod slide down on an inclined plane of inclination 37^o as shown in figure. If coefficient of friction of m_1 and m_2 with inclined plane are mu_1 = 0.75 and mu_2 = 0.25 respectively, then tension (T) in the rod is (g = 10 ms^-2 )

A block of mass 5 kg is kept on a rough horizontal surface. The coefficient of friction for the contact force block and surface are mu_(s) = 0*1 and mu_(k) = 0*9 respectively . A horizontal force F given by F 0*5t is applied at t = 0 . Here t represent time in seconds . Determine the force of friction and acceleration of the block at (i) t = 1s (ii) t= 10 s (iii) t = 12 s

The two blocks A and B of equal mass are initially in contact when released from rest on the inclined plane. The coefficients of friction between the inclined plane and A and B are mu_(1) and mu_(2) respectiely. Friction is not sufficient to prevent slipping.

Figure shown two blocks in contact sliding down an inclined surface of inclination 30^(@) . The friction coefficient between block of mass 2 kg and the incline is mu_(1) = 0.20 and that between the block of mass 4kg and the incline is mu_(2) = 0.30 .Find the acceleration of 2.0 kg block g = 10 ms^(-2)

In the arrangement shown in figure coefficient of friction between 5kg block and incline plane is mu=0.5. Friction force acting on the 5kg block is A. 20N B. 10N C. 15N D. 5N

A force of 750 N is applied to a block of mass 102 kg to prevent it from sliding on a plane with an inclination angle 30^@ with the horizontal. If the coefficients of static friction and kinetic friction between the block and the plane are 0.4 and 0.3 respectively, then the frictional force acting on the block is

In Fig the block are at rest a force of 10 N act on the block of 4 kg mass .The coefficient of staic friction and the coefficient of kinetic friction are mu_(s) = 0.2 and mu_(s) = 0.15 for both the surface in contact The magnitudeof frcition force acting between the surface of contact between the 2 kg and 4 kg block in this situation is

Coefficient of kinetic friction and coefficient of static friction between two blocks is mu_(k) and mu_(s) respectively. In general

The block of mass m_(1) is placed on a wedge of an angle theta , as shown. The block is moving over the inclined surface of the wedge. Friction coefficient between the block and the wedge is mu_(1) , whereas it is mu_(2) between the wedge and the horizontal surface. if mu_(1)=1/2, theta=45^(@), m_(1)=4 kg, m_(2)=5 kg and g=10 m//s^(2) , find minimum value of mu_(2) so that the wedge remains stationary on the surface. express your answer in multiple of 10^(-3)