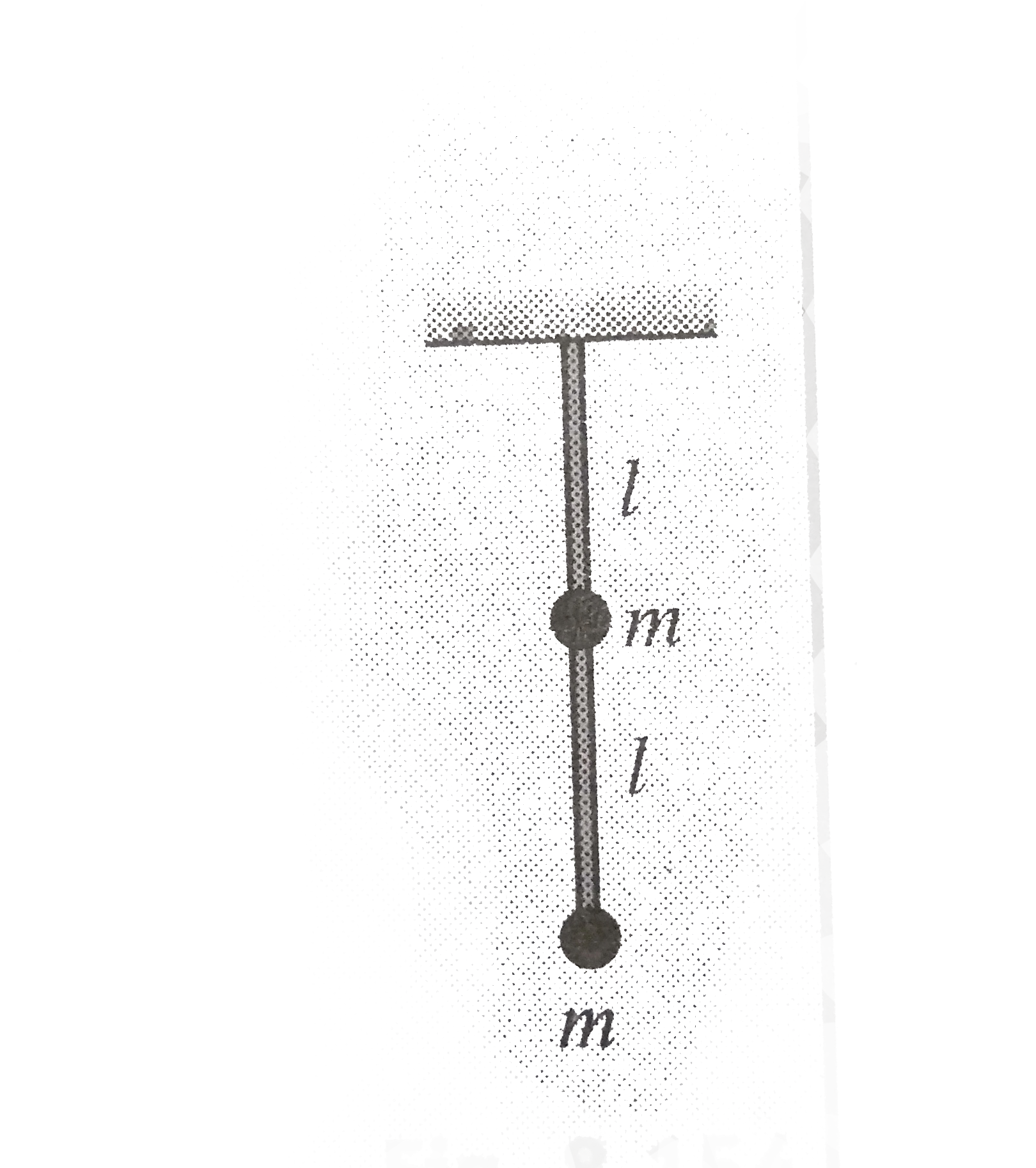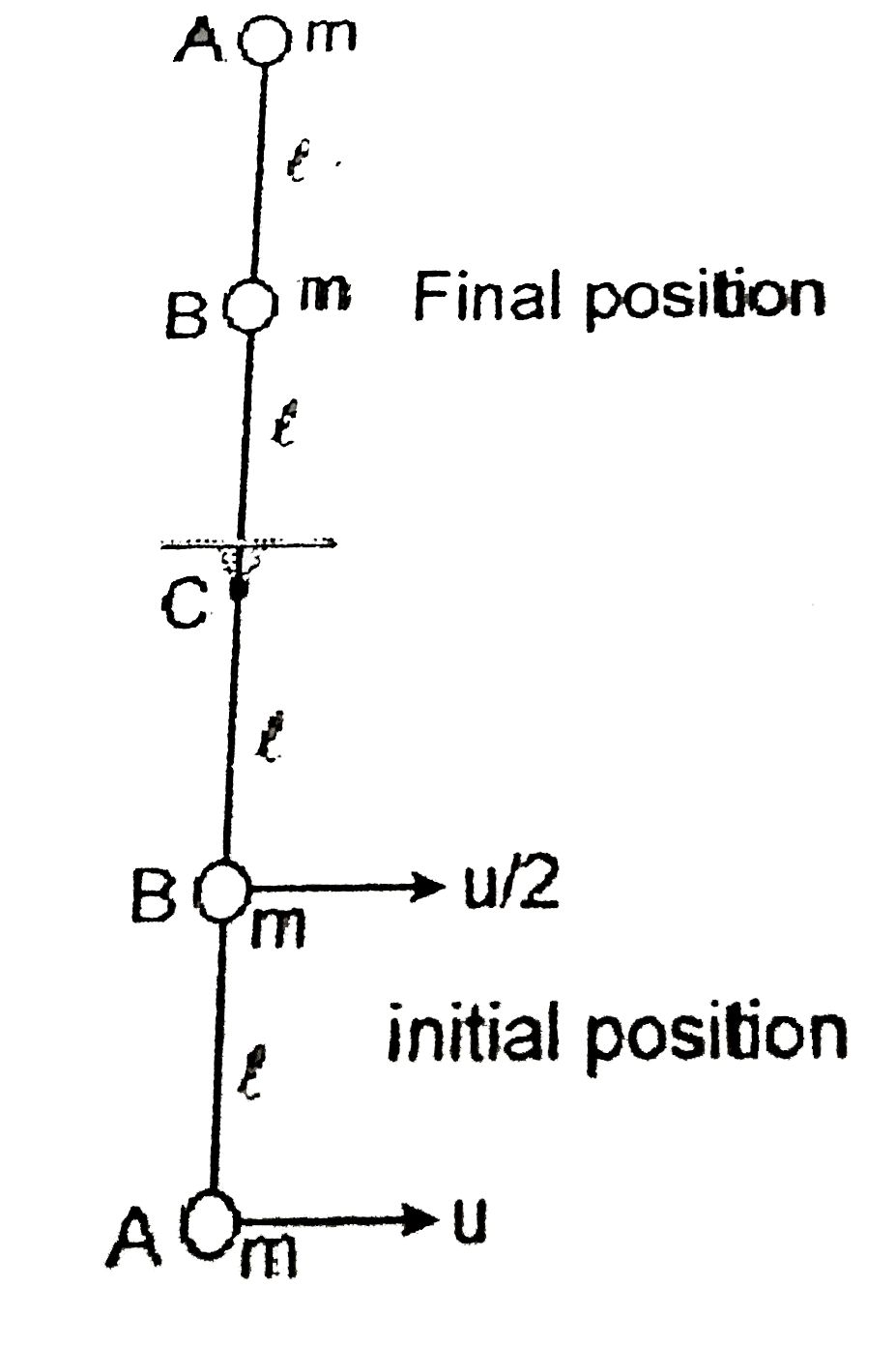Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 44|5 VideosDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise DPP 45|7 VideosDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 42|7 VideosCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise Exercise|53 VideosELASTICITY AND VISCOCITY
RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEMS-dpp 43
- A block of mass 1kg slides down a curved track which forms one quadran...
Text Solution
|
- A bead of mass m slides without friction on a vertical hoop of radius ...
Text Solution
|
- In a simple pendulum, the breaking strength of the string is double th...
Text Solution
|
- A particle of mass m initially at rest starts moving from point A on t...
Text Solution
|
- A heavy particle is projected from a point on the horizontal at an ang...
Text Solution
|
- Two point masses m are connected the light rod of length l and it is f...
Text Solution
|
- A smooth sphere (mass 10kg. negligible radius) rolls on a smooth curv...
Text Solution
|
- A smooth sphere (mass 10kg. negligible radius) rolls on a smooth curv...
Text Solution
|
- A smooth sphere ( mass 10kg. negligible radius ) rolls on a smooth cu...
Text Solution
|
- A smooth sphere ( mass 10kg. negligible radius ) rolls on a smooth cu...
Text Solution
|
- A smooth sphere ( mass 10kg. negligible radius ) rolls on a smooth cu...
Text Solution
|