Home
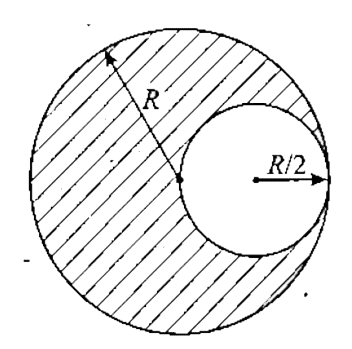
Class 11
PHYSICS
From the circular disc of radius 4R two ...

From the circular disc of radius `4R` two small discs of radius R are cut off. The centre of mass of the new structure will be at

A

`hat(i)(R)/(5)+hat(j)(R)/(5)`

B

`-hat(i)(R)/(5)+hat(j)(R)/(5)`

C

`-hat(i)(R)/(5)-hat(j)(R)/(5)`

D

`-(3R)/(14)(hat(i)+hat(j))`

Text Solution

Verified by Experts

The correct Answer is:
D
Centre of mass of circular disc of radius
`4R=(0,0)`
Centre of mass of upper disc `=(0,3R)`
Centre of mass lower disc `=(3R,0)`
Let `M` be mass of complete disc and then the mass of cut out disc are `(M)/(16)`
Hence, centre of mass of new structure is given by
`bar (x)=(m_(1)x_(1)-m_(2)x_(2)-m_(3)x_(2))/(m_(1)-m_(2)-m_(3))`
`=(M(0)-(M)/(16)(3r)-(M)/(16)(0))/(M-(M)/(16)-(M)/(16))=(-3R)/(14)`
Position vector of `C.M. =-(3R)/(14)(hat(i)+hat(j))`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise DPP 45|7 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 46|6 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 43|11 Videos

  • CURRENT ELECTRICITY

    RESONANCE ENGLISH|Exercise Exercise|53 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)

From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)

From a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

From a uniform disc of radius R , a circular section of radius R//2 is cut out. The centre of the hole is at R//2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.

From a circular disc of radius R , a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is -

From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

A circular disc of radius R is removed from a bigger circular disc of radius 2 R such that the circumferences of the discs coincide. The center of mass of new disc is alpha R from the center of the bigger disc. The value of alpha is

A uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?

A uniform metal disck of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be

Figure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R//2 . Find the centre of mass of the remaining part of the disc.