Home
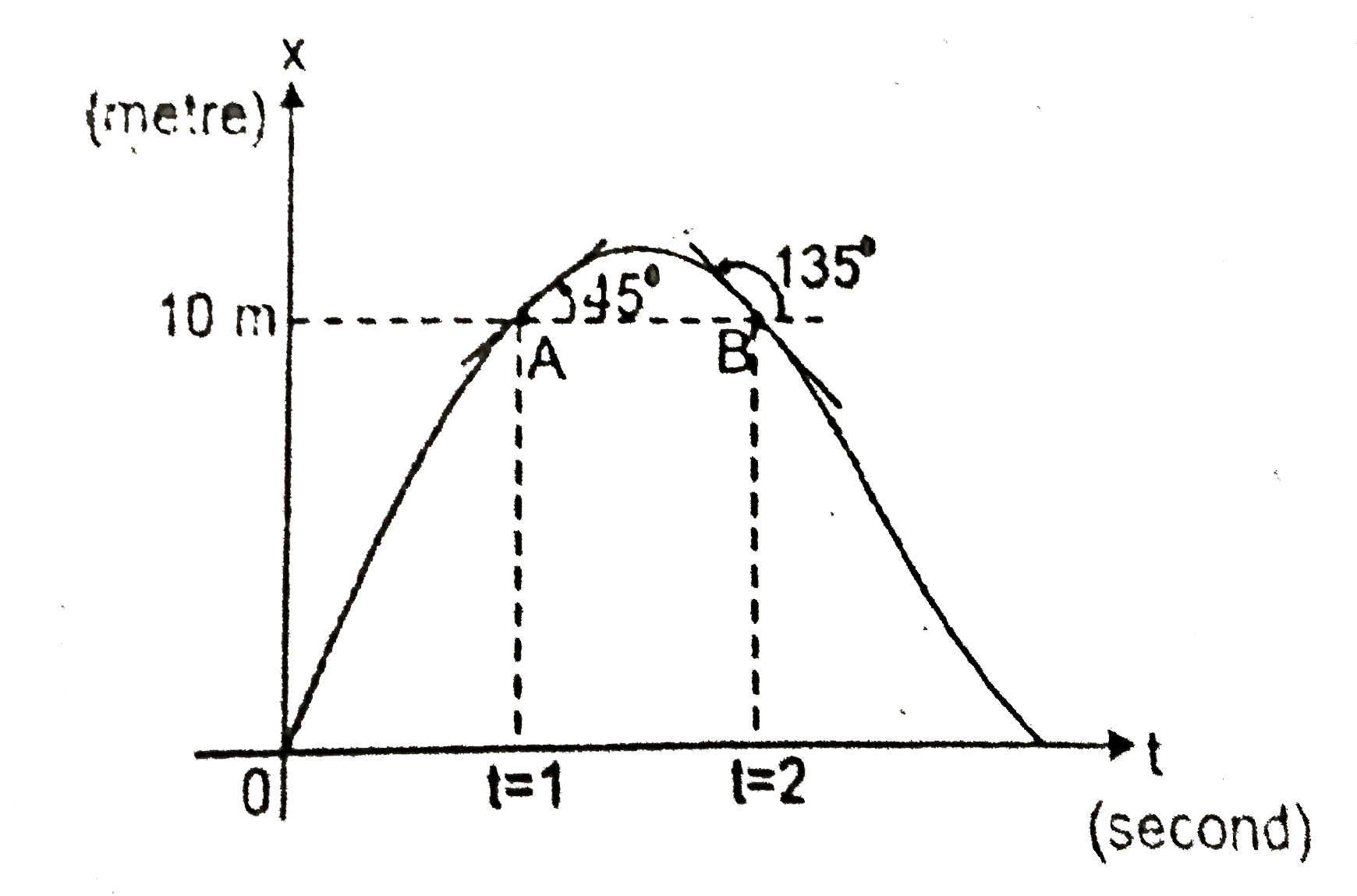
Class 11
PHYSICS
Displacement - time curve of a particle ...

Displacement `-` time curve of a particle moving along a straigh line is shown. Tangents at `A` and `B` make angles `45^(@)` and `135^(@)` with positive `x-` axis respectively. The average acceleratively. The average acceleration of the particle during `t=1,t=2` second is `:`

A

`-2m//s^(2)`

B

`1m//s^(2)`

C

`-1m//s^(2)`

D

zero

Text Solution

Verified by Experts

The correct Answer is:
A
`a_(av)=(V_(f)-V_(i))/(Deltat)=(("Slope at B")-("Slope at A"))/(1s)=(-1-1)/(1)=-2m//s^(2)`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 51|7 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 52|7 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 49|6 Videos

  • CURRENT ELECTRICITY

    RESONANCE ENGLISH|Exercise Exercise|53 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

Displacement-time curve of a particle moving along a straight line is shown. Tangents at A and B makes angle 45^(@) and 135^(@) with positive x -axis respectively. The average acceleration of the particle during t=1,t=2 seconds is

The x-t graph of a particle moving along a straight line is shown in figure The v-t graph of the particle is correctly shown by

The x-t graph of a particle moving along a straight line is shown in figure The a-t graph of the particle is correctly shown by

Acceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :-

The velocity - time graph of a particle moving along a straight line is shown in the figure given below The displacement of the particle in 5 second is

The x-t graph of a particle moving along a straight line is shown in figure The speed-time graph of the particle is correctly shown by

The position (x) - time (t) graph for a particle moving along a straight line is shown in figure. The average speed of particle in time interval t = 0 to t = 8 s is

A particle is moving along straight line whose position x at time t is described by x = t^(3) - t^(2) where x is in meters and t is in seconds . Then the average acceleration from t = 2 sec. to t = 4 sec, is :

Average velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.

Average velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.