Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.33|20 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.34|9 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.31|20 VideosCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise High Level Problems (HIP)|19 VideosELECTRO MAGNETIC WAVES
RESONANCE ENGLISH|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEM-DPP No.32
- A car is moving along a circle with constant speed on an inclined pla...
Text Solution
|
- A block of density 2000 kg//m^(3) and mass 10 kg is suspended by a spr...
Text Solution
|
- A horizontal cylinder is fixed, its inner surface is smooth and its ra...
Text Solution
|
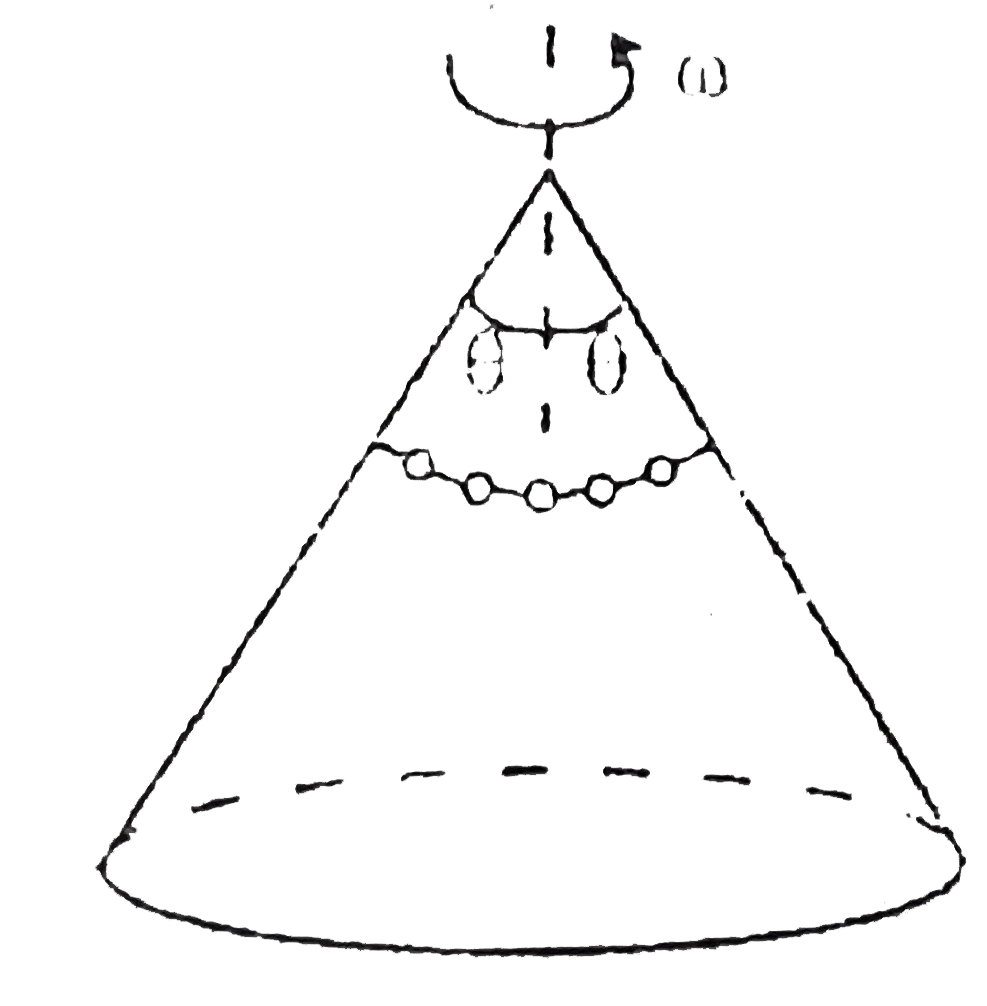
- A chain of mass 'm' and radius 'r' is placed onto a cone of semi verti...
Text Solution
|
- Two coaxial rings, eacg of radius R, made of thin wire are separated b...
Text Solution
|
- An infinitely large non-conducting plane of uniform surface charge den...
Text Solution
|
- A tank of height H and base area A is half filled with water and there...
Text Solution
|
- A tank of height H and base area A is half filled with water and there...
Text Solution
|
- A tank of height H and base area A is half filled with water and there...
Text Solution
|